MIDPOINT OF THE LINE SEGMENT BETWEEN TWO AXIS

Question 1 :

If P(r, c) is mid point of a line segment between the axes, then show that (x/r) + (y/c) = 2.

Solution :

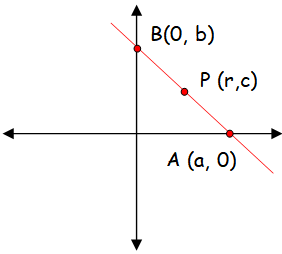
Midpoint of the line segment  =  (r, c)

(x₁ + x₂)/2, (y₁ + y₂)/2  =  (r, c)

(a + 0)/2, (0 + b)/2  =  (r, c)

a/2  =  r     b/2  =  c

a =  2r and b = 2c

Equation of the line 

x/a + y/b  =  1

x/2r + y/2c  =  1

x/r + y/c  =  2

Question 2 :

Find the equation of the line passing through the point (1, 5) and also divides the co-ordinate axes in the ratio 3:10.

Solution :

Let A (a , 0) and B(0, b) are the points on the coordinate axis

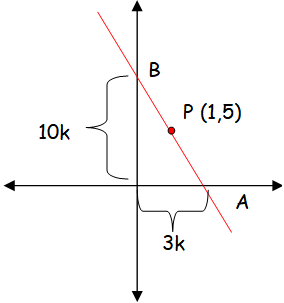
The required line is passing through the point (1, 5).

Here a = 3k and b = 10k

x/a + y/b  =  1

1/3k + 5/10k  =  1

1/3k + 1/2k  =  1

(2 + 3)/6k  =  1

k  =  5/6

a  =  3(5/6)  =  5/2 and b = 10k = 10(5/6)  =  25/3

x/(5/2) + y/(25/3)  =  1

(2x/5) + (3y/25)  =  1

 10x + 3y  =  25

Question 3 :

If p is length of perpendicular from origin to the line whose intercepts on the axes are a and b, then show that 1/p² = 1/a² + 1/b² .

Solution :

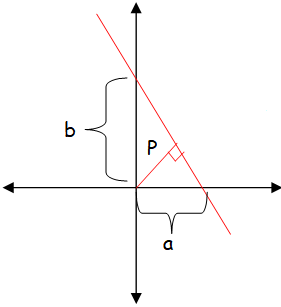
Equation of the given line is x/a + y/b =  1

Now let us find the distance between the point origin to the line x/a + y/b - 1 = 0

d  =  |Ax + By + C|/√A² + B²

A  =  Coefficient of x in the given line  =  1/a

B  =  Coefficient of y in the given line  =  1/b

C  =  -1

P  =  |(1/a)x + (1/b)y - 1|/√(1/a)² + (1/b)²

Since the line is passing through the (0, 0)

P  =  |(1/a)0 + (1/b)0 - 1|/√(1/a)² + (1/b)²

p  =  1/√(1/a)² + (1/b)²

Taking squares and reciprocals on both sides,

1/p²  =  (1/a)² + (1/b)²

1/p²  =  (1/a²) + (1/b²)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.