MINIMUM AND MAXIMUM OF ABSOLUTE VALUE FUNCTION

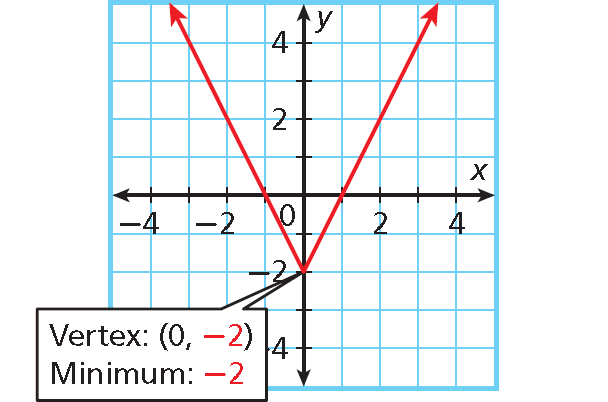
Minimum Value of an Absolute Value Function

If the graph of an absolute value function opens upward, the y-value of the vertex is the minimum value of the function.

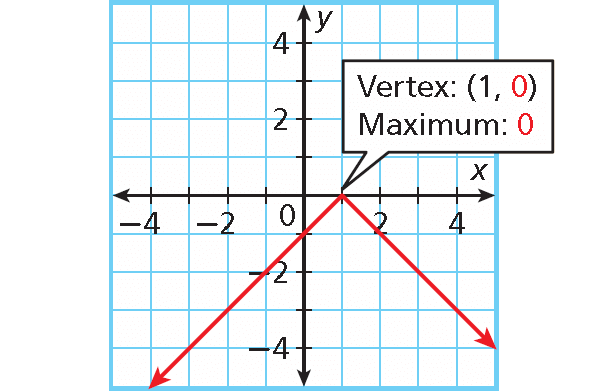
Maximum Value of an Absolute Value Function

If the graph of an absolute value function opens downward, the y-value of the vertex is the maximum value of the function.

Solved Examples 

Example 1 :

Describe the transformations from the graph of f(x) = |x| to the graph of g(x). Identify the vertex of g(x) and give the minimum or maximum value.

g(x)  =  2|x + 1|

Solution :

Identify a, b, and c.

g(x) = 2|x + 1| = 2|x – (–1)| + 0.

• a = 2 : graph is narrower

• b = –1 : translated 1 unit left

• c = 0 : no vertical translation

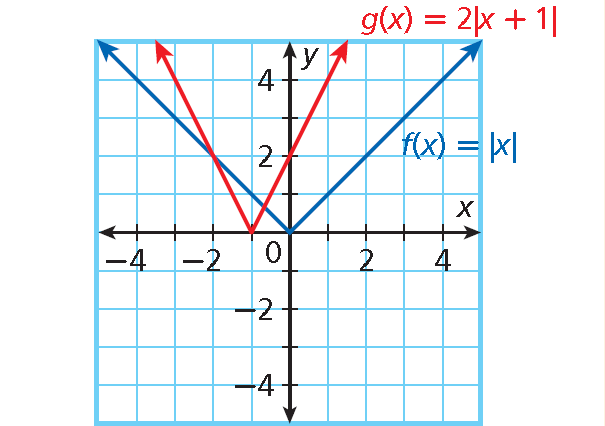
The vertex of g(x) is (–1, 0).

The graph opens upward, so the function has minimum  value.

The minimum value is 0.

Example 2 :

Describe the transformations from the graph of f(x) = |x| to the graph of g(x). Identify the vertex of g(x) and give the minimum or maximum value.

g (x)  =  -|x - 3| + 2

Solution :

Identify a, b, and c.

g(x) = -|x - 3| + 2 = -1|x – 3| + 2.

• a = -1 : graph opens downward and width is unchanged

• b = 3 : translated 3 units right

• c = 2 : translated 2 units up

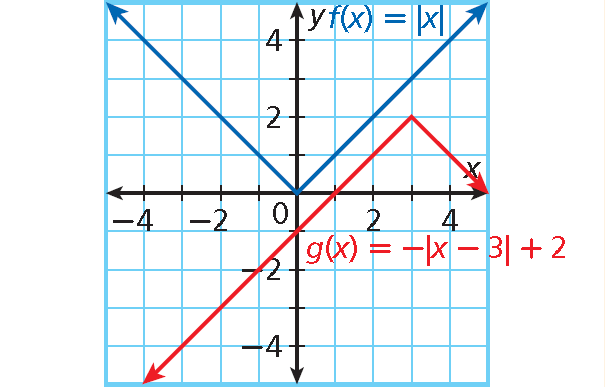
The vertex of g(x) is (3, 2).

The graph opens downward, so the function has maximum  value.

The maximum value is 2.

Example 3 :

Graph f(x) = |x + 3| – 5. Identify the vertex and give the minimum or maximum value of the function.

Solution :

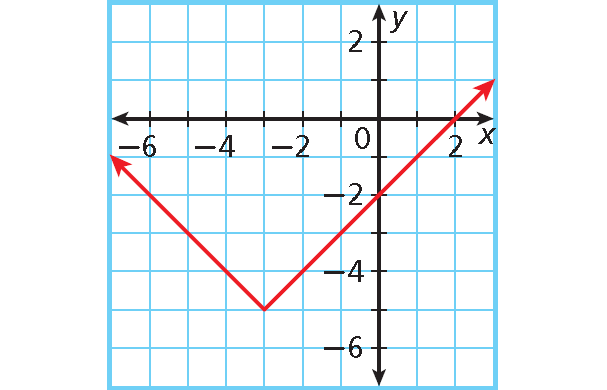
The vertex is (–3, –5).

The graph opens upward, so the function has minimum  value.

The minimum value is –5.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.