MODELING INTEGER MULTIPLICATION WITH COUNTERS

Counters representing positive and negative integers can help us to understand how we find the product of two negative integers.

Counters we use to model integer multiplication : 

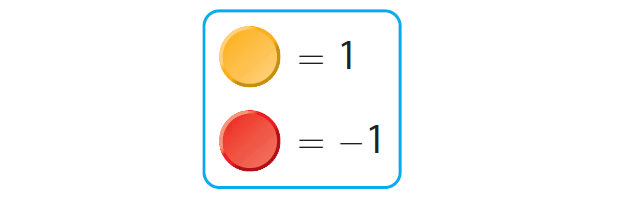
Example 1 :

Find the product of 3 and -4. 

Solution : 

We have to find 3(-4)

Step 1 : 

Here, the second number is negative (-4).

So, use negative counters to model 3(-4).

Step 2 :

In the above picture, there are three groups of "-4". 

In total, there are 12 negative counters. 

3(-4)  =  -12

So, the product of 3 and -4 is -12. 

Example 2 :

Find the product of 3 and 4. 

Solution : 

We have to find 3(4).

Step 1 : 

Here, the second number is positive (4).

So, use positive counters to model 3(4).

Step 2 :

In the above picture, there are three groups of "4". 

In total, there are 12 positive counters. 

3(4)  =  12

So, the product of 3 and 4 is 12. 

Example 3 :

Find the product of -3 and -4. 

Solution : 

Write (-3)(-4) as -3(-4), which means the opposite of 3(-4).

Step 1 : 

Here, the second number is negative (-4).

So, use negative counters to model 3(-4).

In the above picture, there are three groups of "-4". 

Step 2 :

Now, we have to make the same model using positive counters to find the opposite of 3(-4).

Step 3 :

Translate the model into a mathematical expression :

(-3)(-4)  =  12

So, the product of -3 and -4 is 12.

Example 4 :

What do you notice about the sign of the product of two negative integers ?

Solution : 

When we find the product of two negative integers, always the result is positive.

Example 5 :

What can we conclude about the sign of the product of two integers with the same sign?

Solution : 

If the original integers are positive, the product is positive. If they are negative, the product is positive. So, the product of two integers with the same sign is always positive.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.