MULTIPLE REPRESENTATIONS OF RELATIONS WORKSHEET

Problem 1 : 

In the scoring system of some track meets, first place is worth 5 points, second place is worth 3 points, third place is worth 2 points, and fourth place is worth 1 point. This scoring system is a relation, so it can be shown as ordered pairs, {(1, 5), (2, 3), (3, 2), (4, 1)}. Express the relation for the track meet scoring system as a table, as a graph, and as a mapping diagram.

1. Answer :

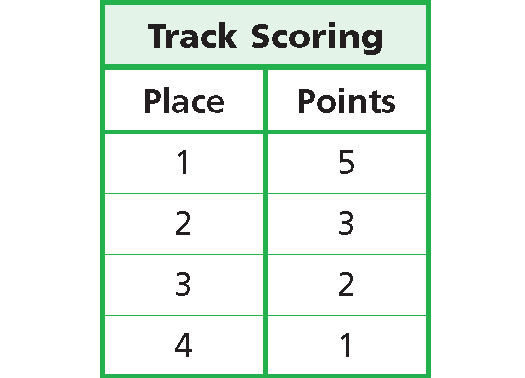
Table : 

Write all x-values under “Place” and all y-values under “Points.”

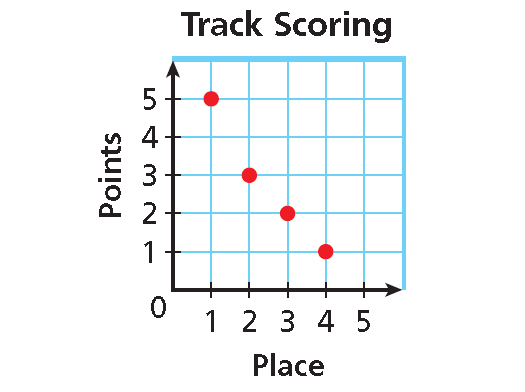
Graph : 

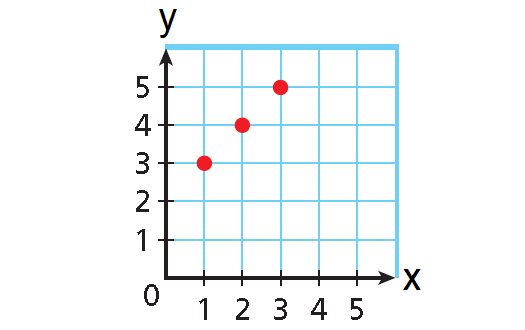
Use the x- and y-values to plot the ordered pairs.

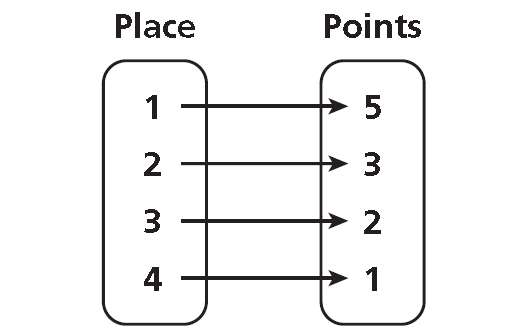
Mapping Diagram : 

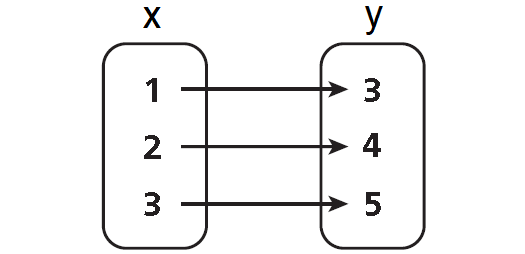
Write all x-values under “Place” and all y-values under “Points.” Draw an arrow from each x-value to its corresponding y-value.

Problem 2 : 

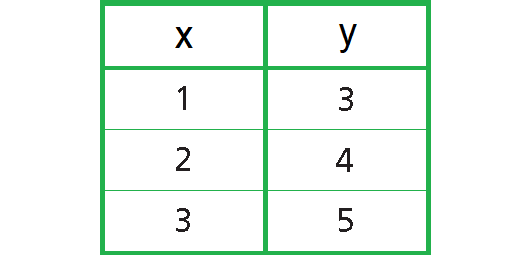
Express the relation {(1, 3), (2, 4), (3, 5)} as a table, as a graph, and as a mapping diagram.

2. Answer : 

Table : 

Graph : 

Mapping Diagram : 

Problem 3 : 

A = {1, 2, 3, 4} and B = {2, 5, 8, 11, 14} be two sets.

Let f : A--->B be a relation given by f(x) = 3x −1.

Represent this relation 

(i) by arrow diagram

(ii) in a table form

(iii) as a set of ordered pairs

(iv) in a graphical form

3. Answer : 

A = {1, 2, 3, 4}; B = {2, 5, 8, 11, 14}; f (x) = 3x −1

Arrow Diagram : 

Let us represent the relation f : A--->B by an arrow diagram. 

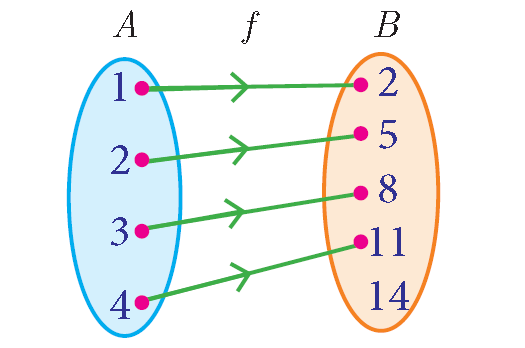
Table Form :

The given relation f can be represented in a tabular form as shown below

Set of Ordered Pairs :

The relation f can be represented as a set of ordered pairs as

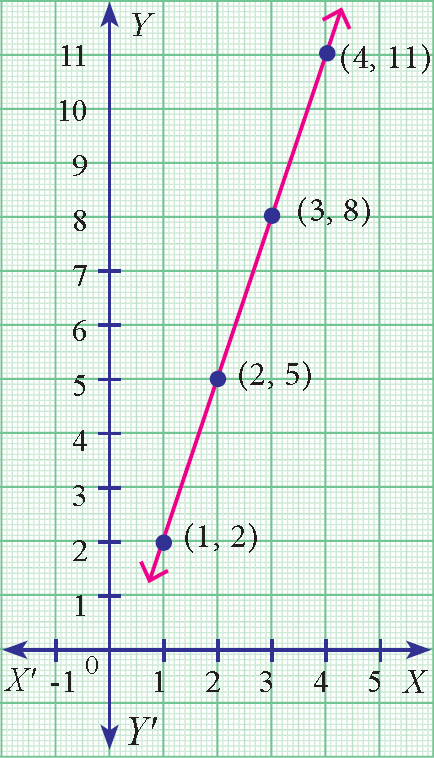
f  =  {(1, 2), (2, 5), (3, 8), (4, 11)}

Graphical Form :

To get the graphical form of the given relation, plot the points (1, 2), (2, 5), (3, 8), (4, 11) on a xy-plane. 

Problem 4 :

An aerobics class is being offered once a week for 6 weeks. The registration fee is $15 and cost of each class attended is $10. Write the function rule to describe the total cost of the class. Find the reasonable domain and range of the function.

Solution :

Registration fee = $15

Cost to be paid for each class = 10

Let x be the number of classes attending.

Let f(x) be the total cost.

f(x) = 15 + 10x

So, the required function f(x) = 10x + 15

Domain = 0 ≤ x < ∞

Range = 15 ≤ y < ∞

Problem 5 :

A fitness class is being offered twice a week for four weeks. The registration fee is $8.50 and the cost for each class attended $4.75. Write the function rule to describe the total cost of the class. Find the reasonable domain and range of the function.

Solution :

Registration fee = $8.50

Cost to be paid for each class = $4.75

Let x be the number of classes attending.

Let f(x) be the total cost.

f(x) = 8.50 + 4.75x

So, the required function f(x) = 8.50 + 4.75x

Domain = 0 ≤ x < ∞

Range = 8.50 ≤ y < ∞

Identify the dependent and independent variables for each situation given below. Write the function. Then evaluate the function for the given input values.

Problem 6 :

The Limo service charges $90 for each hour.

Evaluate for x = 2

Solution :

Let x be the number of hours.

Let y be the total cost.

Charge for each hour = $90

Required function y = 90x

Dependent variable = y

Independent variable = x

When x = 2, y = 90(2) ==> 180

Charge for 2 hours is $180

Problem 7 :

A computer support company charges $295 for the first four plus $95 for each additional hour.

Solution :

Let x be each additional hour.

Company charge = $295 (for first four hours)

Charge for each additional hour = 95

Let y be the total cost.

y = 295 + 95x

Dependent variable = y

Independent variable = x

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.