MULTIPLYING RATIONAL EXPRESSIONS
How to multiply rational expressions :
1. Multiply numerators and denominators.
2. Factor the numerator and denominator.
3. Cancel common factors to simplify.
Multiply the rational expressions and show the product in simplest form :
Example 1 :
[(x2 - 2x)/(2x + 4)] ⋅ [(3x + 6)/(5x - 10)]
Solution :
= [(x2 - 2x)/(2x + 4)] ⋅ [(3x + 6)/(5x - 10)]
Multiply numerators and denominators.
= [(x2 - 2x)(3x + 6)] /[(2x + 4)(5x - 10)]
Factor the numerator and denominator.
= [x(x - 2)3(x + 2)] /[2(x + 2)5(x - 2)]
= [3x(x - 2)(x + 2)] /[10(x + 2)(x - 2)]
Cancel common factors.
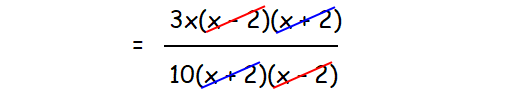
= 3x/10
Example 2 :
[(6x + 6)/(x2 - 4)] ⋅ [(x2 + 6x + 8)/(3x + 3)]
Solution :
= [(6x + 6)/(x2 - 4)] ⋅ [(x2 + 6x + 8)/(3x + 3)]
Multiply numerators and denominators.
= [(6x + 6)(x2 + 6x + 8)] / [(x2 - 4)(3x + 3)]
Factor the numerator and denominator.
= [6(x + 1)(x + 2)(x + 4)] / [(x + 4)(x - 4)3(x + 1)]
= [6(x + 1)(x + 2)(x + 4)] / [3(x + 4)(x - 4)(x + 1)]
Cancel common factors.
= [6(x + 2)] / [3(x - 4)]
= 2(x + 2)/(x - 4)
Example 3 :
[(a + b)/(a - b)] ⋅ [(a3 - b3)/(a3 + b3)]
Solution :
= [(a + b)/(a - b)] ⋅ [(a3 - b3)/(a3 + b3)]
Multiply numerators and denominators.
= [(a + b)(a3 - b3)]/[(a - b)(a3 + b3)]
Factor the numerator and denominator.
= [(a + b)(a - b)(a2 + ab + b2)]/[(a - b)(a + b)(a2 - ab + b2)]
Cancel common factors.
= (a2 + ab + b2) / (a2 - ab + b2)
Example 4 :
(5ab/15cd) ⋅ (4bc/32ad) ⋅ (16ac/2bc)
Solution :
= (5ab/15cd) ⋅ (4bc/32ad) ⋅ (16ac/2bc)
Multiply numerators and denominators.
= (5ab ⋅ 4bc ⋅ 16ac) / (15cd ⋅ 32ad ⋅ 2bc)
= 320a2b2c2 / 960abc2d2
Cancel common factors.
= ab/3d2
Example 5 :
[(x2 - 2x + 1)/(x2 - 3x + 2)] ⋅ [(3x - 6)/(6x - 6)]
Solution :
= [(x2 - 2x + 1)/(x2 - 3x + 2)] ⋅ [(3x - 6)/(6x - 6)]
Multiply numerators and denominators.
[(x2 - 2x + 1)(3x - 6)] / [(x2 - 3x + 2)(6x - 6)]
Factor the numerator and denominator.
= [(x - 1)(x - 1)3(x - 2)] / [(x - 2)(x - 1)6(x - 1)]
= [3(x - 1)(x - 1)(x - 2)] / [6(x - 2)(x - 1)(x - 1)]
Cancel common factors.
= 3/6
= 1/2
Example 6 :
[(x2 - 25)/(x + 3)] ⋅ [(x2 - 9)/(x + 5)2]
Solution :
= [(x2 - 25)/(x + 3)] ⋅ [(x2 - 9)/(x + 5)2]
Multiply numerators and denominators.
= [(x2 - 25)(x2 - 9)] ⋅ [(x + 3)(x + 5)2]
Factor the numerator and denominator.
= [(x + 5)(x - 5)(x + 3)(x - 3)] / [(x + 3)(x + 5)(x + 5)]
Cancel common factors.
= [(x - 5)(x - 3)] / (x + 5)
Example 7 :
[(x2 - 9y2)/(3x - 3y)] ⋅ [(x - y)/(x + 3y)]
Solution :
= [(x2 - 9y2)/(3x - 3y)] ⋅ [(x - y)/(x + 3y)]
Multiply numerators and denominators.
= [(x2 - 9y2)(x - y)] / [(3x - 3y)(x + 3y)]
Factor the numerator and denominator.
= [(x + 3y)(x - 3y)(x - y)] / [3(x - y)(x + 3y)]
Cancel common factors.
= (x - 3y)/3
Example 8 :
[(x2 - 16)/(x - 2)] ⋅ [(x - 2)/(x3 + 64)]
Solution :
= [(x2 - 16)/(x - 2)] ⋅ [(x - 2)/(x3 + 64)]
Multiply numerators and denominators.
= [(x2 - 16)(x - 2)] / [(x - 2)(x3 + 64)]
= [(x2 - 42)(x - 2)] / [(x - 2)(x3 + 43)]
Factor the numerator and denominator.
= [(x + 4)(x - 4)(x - 2)] / [(x - 2)(x + 4)(x2 - 4x + 16)]
Cancel common factors.
= (x - 4)/(x2 - 4x + 16)
Example 9 :
[(p2 - 1)/p] ⋅ [p3/(p - 1)] ⋅ [1/(p + 1)]
Solution :
= [(p2 - 1)/p] ⋅ [p3/(p - 1)] ⋅ [1/(p + 1)]
Multiply numerators and denominators.
= [(p2 - 1) ⋅ p3 ⋅ 1] / [p(p - 1)(p + 1)]
= p3(p2 - 1) / p(p2 - 12)
= p3(p2 - 1) / p(p2 - 1)
Cancel common factors.
= p2
Example 10 :
[(px - 2p)/(qx - 3q)] ⋅ [(bx - 3b)/(ax - 2a)]
Solution :
= [(px - 2p)/(qx - 3q)] ⋅ [(bx - 3b)/(ax - 2a)]
Multiply numerators and denominators.
= [(px - 2p)(bx - 3b)] / [(qx - 3q)(ax - 2a)]
Factor the numerator and denominator.
= [p(x - 2)b(x - 3)] / [q(x - 3)a(x - 2)]
= [bp(x - 2)(x - 3)] / [aq(x - 3)(x - 2)]
Cancel common factors.
= bp/aq

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
SAT Math Resources (Videos, Concepts, Worksheets and More)
Nov 16, 24 08:15 AM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Digital SAT Math Problems and Solutions (Part - 71)
Nov 16, 24 08:03 AM
Digital SAT Math Problems and Solutions (Part - 71) -
Digital SAT Math Problems and Solutions (Part - 70)
Nov 15, 24 07:12 PM
Digital SAT Math Problems and Solutions (Part - 70)