MULTIPLYING A POLYNOMIAL BY A MONOMIAL
Using distributive property of multiplication, you can multiply a polynomial (a + b + c) by a monomial (a) as shown below.
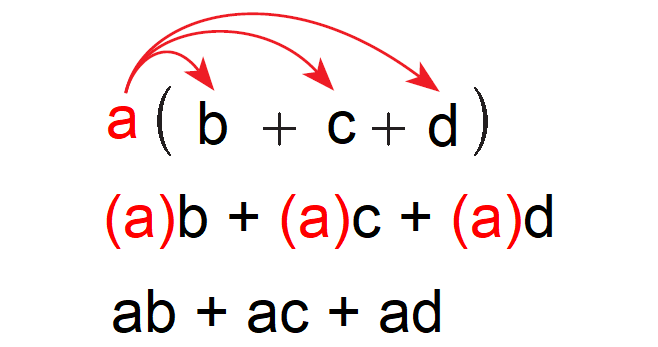
Example 1 :
Multiply.
2(3x2 + 5x + 7)
Solution :
= 2(3x2 + 5x + 7)
Distribute 2.
= 2(3x2) + 2(5x) + 2(7)
Multiply.
= 6x2 + 10x + 14
Example 2 :
Multiply.
-5(2x3 - 5x2 + 7x - 3)
Solution :
= -5(2x3 - 5x2 + 7x - 3)
Distribute -5.
= -5(2x3) - 5(-5x2) - 5(7x) - 5(-3)
Multiply.
= -10x3 + 25x2 - 35x + 15
Example 3 :
Multiply.
2x2y(4x - y)
Solution :
= 2x2y(4x - 3y)
Distribute 2x2y.
= 2x2y(4x) + 2x2y(-3y)
Group like terms together.
= (2 ⋅ 4)(x2 ⋅ x)(y) + 2(-3)(x2)(y ⋅ y)
Use the Product of Powers Property.
= 8x2 + 1y - 6x2y1 + 1
= 8x3y - 6x2y2
Example 4 :
Multiply.
5a(a2b + 3b2)
Solution :
= 5a(a2b + 3b2)
Distribute 5a.
= 5a(a2b) + 5a(3b2)
Group like terms together.
= 5(a ⋅ a2)b + (5 ⋅ 3)ab2
Use the Product of Powers Property.
= 5a1 + 2b + 15ab2
= 5a3b + 15ab2
Example 5 :
Multiply.
3ab(5a2 + b)
Solution :
= 3ab(5a2 + b)
Distribute 3ab.
= 3ab(5a2) + 3ab(b)
Group like terms together.
= (3 ⋅ 5)(a ⋅ a2)b + 3a(b ⋅ b)
Use the Product of Powers Property.
= 15a1 + 2b + 3ab1 + 1
= 15a3b + 3ab2
Example 6 :
Multiply.
-2a2b3(3ab2 - a2b)
Solution :
= -2a2b3(3ab2 - a2b)
Distribute -2a2b3.
= -2a2b3(3ab2) - 2a2b3(-a2b)
Group like terms together.
= -(2 ⋅ 3)(a2 ⋅ a)(b3 ⋅ b2) - (2 ⋅ -1)(a2 ⋅ a2)(b3 ⋅ b)
Use the Product of Powers Property.
= -6a2 + 1b3 + 2 - (-2)a2 + 2b3 + 1
= -6a3b5 + 2a4b4
Example 7 :
Multiply.
2xy(x2y + xz - xy)
Solution :
= 2xy(x2y + xz - xy)
Distribute 2xy.
= 2xy(x2y) + 2xy(xz) + 2xy(-xy)
Group like terms together.
= 2(x ⋅ x2)(y ⋅ y) + 2(x ⋅ x)yz + 2(-1)(x ⋅ x)(y ⋅ y)
Use the Product of Powers Property.
= 2x1 + 2y1 + 1 + 2x1 + 1yz - 2x1 + 1y1 + 1
= 2x3y2 + 2x2yz - 2x2y2
Example 8 :
Multiply.
2a2b(ab2 - a2b + ab)
Solution :
= 2a2b(ab2 - a2b + ab)
Distribute 2a2b.
= 2a2b(ab2) + 2a2b(-a2b) + 2a2b(ab)
Group like terms together.
= 2(a2 ⋅ a)(b ⋅ b2) + (2 ⋅ -1)(a2 ⋅ a2)(b ⋅ b) + 2(a2 ⋅ a)(b ⋅ b)
Use the Product of Powers Property.
= 2a2 + 1b1 + 2 - 2a2 + 2b1 + 1 + 2a2 + 1b1 + 1
= 2a3b3 - 2a4b2 + 2a3b2
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 100)
Jan 14, 25 12:34 AM
Digital SAT Math Problems and Solutions (Part - 100) -
SAT Math Resources (Videos, Concepts, Worksheets and More)
Jan 14, 25 12:23 AM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Best Way to Learn Mathematics
Jan 12, 25 11:03 PM
Best Way to Learn Mathematics