MULTIPLY AND DIVIDE RATIONAL NUMBERS

Multiplication :

To multiply two rational numbers 'a/b' and 'c/d', multiply the numerators and denominators separately as shown below. 

(a/b) ⋅ (c/d)  =  (a ⋅ c) / (b ⋅ d)

Simplify the product to its lowest form.

Division : 

To divide a rational number 'a/b' by another rational number 'c/d', multiply the first rational number 'a/b' by  the multiplicative inverse of the second rational number 'c/d'.

Multiplicative inverse of 'c/d' is 'd/c'. 

(a/b) ÷ (c/d)  =  (a/b) ⋅ (d/c)  =  (a ⋅ d) / (b ⋅ c)

Note :

In case we have mixed fractions, first we have to convert them to improper fractions and do the multiplication and division as explained above.

Example 1 :

Multiply 2/3 and 5/7.

Solution :

=  (2/3) ⋅ (5/7)

Multiply the numerators and denominators. 

=  (2 ⋅ 5) / (3 ⋅ 7)

=  10/21

Example 2 :

Evaluate : 

(4/-11) ⋅ (-22/8)

Solution :

=  (4/-11) ⋅ (-22/8)

Before we multiply numerators and denominators, we can simplify as shown below.

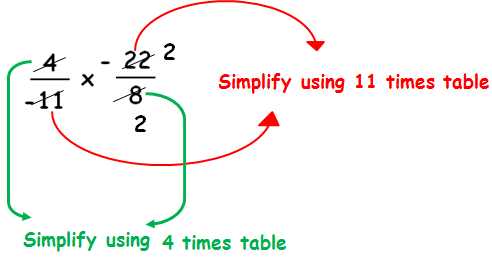
  =  (-2) / (-2)

=  1

Example 3 :

Simplify :

(2/5) ÷ (7/9)

Solution :

  =  (2/5) ÷ (7/9)

To divide by 7/9, multiply by 9/7.

=  (2/5) ⋅ (9/7)

Multiply the numerators and denominators. 

=  (2 ⋅ 9) / (5 ⋅ 7)

=  18/35

Example 4 :

Simplify : 

(-4/9) ÷ (9/-4)

Solution :

  =  (-4/9) ÷ (9/-4)

To divide by 9/-4, multiply by -4/9.

=  (-4/9) ⋅ (-4/9)

Multiply the numerators and denominators. 

=  [(-4)(-4)] / (9 ⋅ 9)

=  16/81

Example 5 :

Multiply 2¼ and 3½.

Solution :

=  (2¼) ⋅ (3½)

Converting the mixed fractions to improper fractions.

=  (9/4) ⋅ (7/2)

=  (9 ⋅ 7) / (4 ⋅ 2)

=  63/8

=  7⅞

Example 6 :

Simplify : 

-9¾ ÷  1⅞

Solution :

=  -9¾ ÷  1⅞

Converting the mixed numbers to improper fractions

=  (-39/4) ÷ (15/8)

To divide by 15/8, multiply by 8/15.

=  (-39/4) ⋅ (8/15)

Simplify 39 and 15 using 3 times table, 4 and 8 using 4 times table. 

=  (-13/1) ⋅ (2/5)

=  (-13 ⋅ 2) / (1 ⋅ 5)

=  -26/5

=  -5⅕

Example 7 :

Find the product of -11/2 and 4/5.

Solution :

  =  (-11/2) ⋅ (4/5)

Multiplying the numerators and denominators.

=  (-11 ⋅ 4) / (2 ⋅ 5)

=  -44/10

=  -22/5

Converting the improper fraction into mixed fraction.

  =  -4⅖

Example 8 :

What is two-fifth of 7/18 ?

Solution :

Two-fifth of 5/18 :

=  (2/5) ⋅ (7/18)

Simplify 2 and 18 using 2 times table.

=  (1/5) ⋅ (7/9)

Multiply numerators and denominators. 

=  (1 ⋅ 7) / (5 ⋅ 9)

=  7/45

Example 9 :

Lily wants to share three-fourth of a pizza equally to 4 of her friends. How much pizza will each friend get ?

Solution :

Amount of pizza each friend will get :

=  (3/4) ÷ 4

=  (3/4) ÷ (4/1)

To divide by 4/1, multiply by 1/4.

=  (3/4) ⋅ (1/4)

Multiply numerators and denominators. 

=  (3 ⋅ 1) / (4 ⋅ 4)

=  3/16

Each friend will get 3/16 of a pizza.  

Example 10 :

Last month, John spent of three-fifth of his salary for food. If John's salary is $5000, how much money did he spend for food ?

Solution :

Money spent for food :

=  (3/5) ⋅ 5000

=  (3/5) ⋅ (5000/1)

Simplify 5 and 5000 using 5 times table.

=  (3/1) ⋅ (1000/1)

Multiply numerators and denominators. 

=  (3 ⋅ 1000) / (1 ⋅ 1)

=  3000/1

=  3000

John spent $3000 for food.  

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.