MULTIPLYING A BINOMIAL BY A BINOMIAL

You can use the following methods to multiply a binomial by a binomial.

(i) Distributive Property.

(ii) FOIL Method

Distributive Property

To multiply a binomial by a binomial, Distributive Property can be used more than once.  

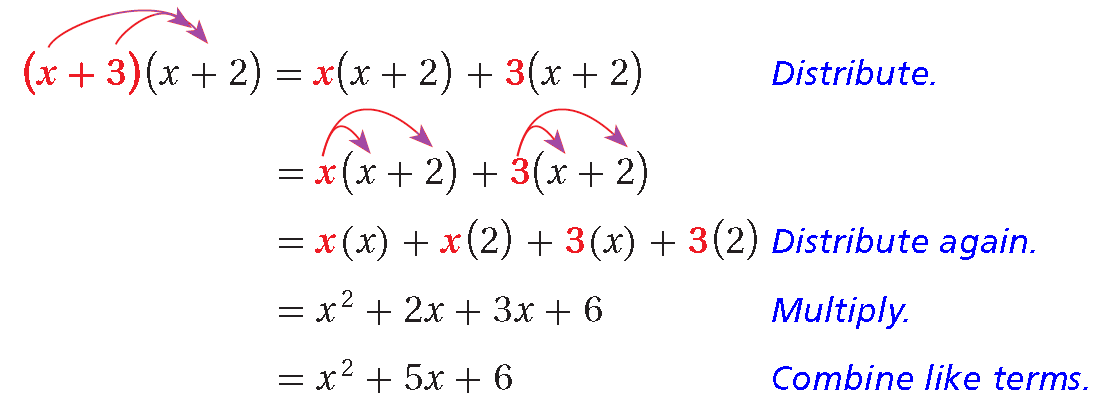
FOIL Method

Another method for multiplying binomials is called the FOIL method. 

1. Multiply the First terms.

2. Multiply the Outer terms.

3. Multiply the Inner terms.

4. Multiply the Last terms.

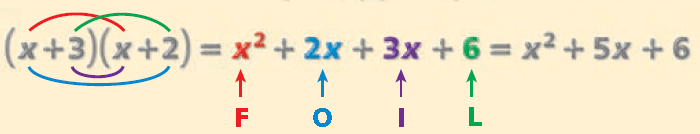
Multiplying Binomials

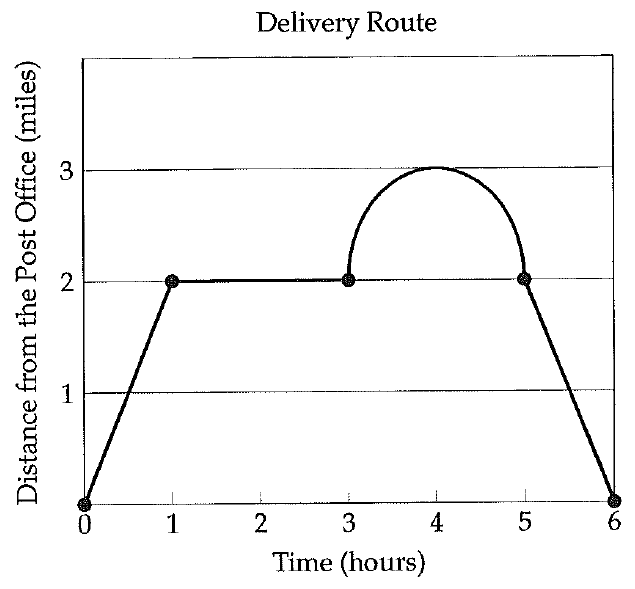
Example 1 : 

Multiply. 

(x + 3)(x - 6)

Solution :

=  (x + 3)(x - 6)

Distribute. 

=  x(x - 6) + 3(x - 6)

Distribute again. 

=  x(x) + x(-6) + 3(x) + 3(-6)

Multiply. 

=  x² - 6x + 3x - 18

Combine like terms. 

=  x² - 3x - 18

Example 2 : 

Multiply. 

(a + b)²

Solution :

=  (a + b)²

Write as a product of two binomials. 

=  (a + b)(a + b)

Distribute. 

=  a(a + b) + b(a + b)

Distribute again. 

=  a(a) + a(b) + b(a) + b(b)

Multiply. 

=  a² + ab + ab + b²

Combine like terms. 

=  a² + 2ab + b²

Example 3 : 

Multiply. 

(p + 5)²

Solution :

=  (p + 5)²

Write as a product of two binomials. 

=  (p + 5)(p + 5)

Use the FOIL method. 

=  (p ⋅ p) + (p ⋅ 5) + (5 ⋅ p) + (5 ⋅ 5)

Multiply. 

=  p² + 5p + 5p + 25

Combine like terms. 

=  p² + 10p + 25

Example 4 : 

Multiply. 

(3b² - c)(b² - 2c)

Solution :

=  (3b² - c)(b² - 2c)

Use the FOIL method. 

=  (3b² ⋅ b²) + (3b²⋅ -2c) + (-c ⋅ b²) + (-c ⋅ -2c)

Multiply. 

=  3b⁴ - 6b²c - b²c + 2c²

Combine like terms. 

=  3b⁴ - 7b²c + 2c²

Example 5 : 

Multiply. 

(2x - y²)(x + 4y²)

Solution :

=  (2x - y²)(x + 4y²)

Use the FOIL method. 

=  (2x ⋅ x) + (2x ⋅ 4y²) + (-y² ⋅ x) + (-y² ⋅ 4y²)

Multiply. 

=  2x² + 8xy² - xy² - 4y⁴

Combine like terms. 

=  2x² - 7xy² - 4y⁴

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.