MULTIPLYING A BINOMIAL BY A TRINOMIAL

To multiply a binomial by a trinomial, you can use the Distributive Property several times. 

Multiply (5x + 3) by (2x² + 10x - 6).

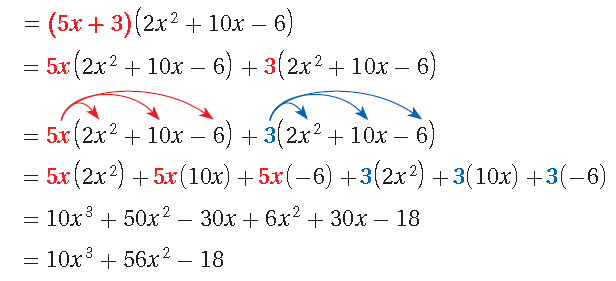
You can also use a rectangle model to multiply a binomial by a trinomial. This is similar to finding the area of a rectangle with length (2x² + 10x - 6) and width (5x + 3).

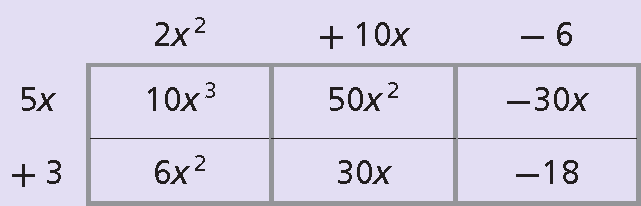
Product of monomials are written in each row and column. 

To find the product, add all of the terms inside the rectangle by combining like terms and simplifying, if necessary.   

=  10x³ + 6x² + 50x² + 30x - 30x - 18

=  10x³ + 56x² - 18

Another method that can be used to multiply a binomial by a trinomial is the vertical method. This is similar to methods used to multiply whole numbers. 

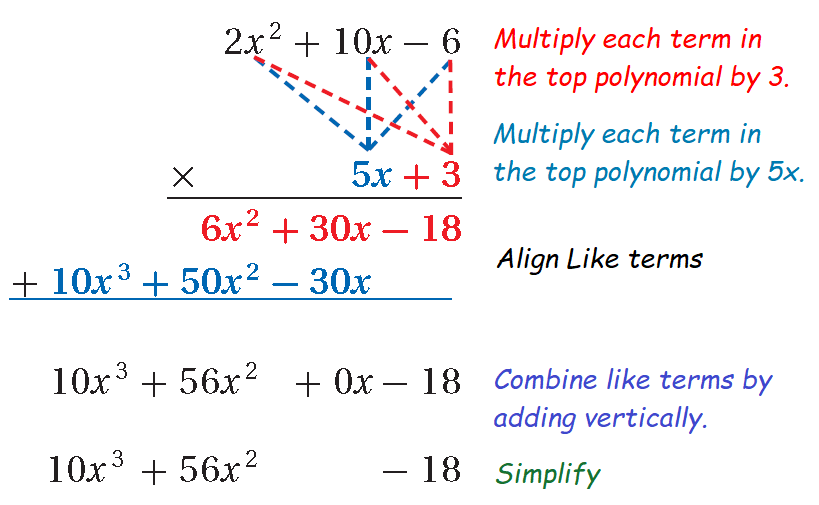
Example 1 :

Multiply.

(x + 3)(x² - 5x + 7)

Answer :

=  (x + 3)(x² - 5x + 7)

Distributive. 

=  x(x² - 5x + 7) + 3(x² - 5x + 7)

Distribute again. 

=  x(x²) + x(-5x) + x(7) + 3(x²) + 3(-5x) + 3(7)

Simplify. 

=  x³ - 5x² + 7x + 3x² - 15x + 21

Combine the like terms.

=  x³ - 5x²  + 3x²+ 7x - 15x + 21

=  x³ - 2x² - 8x + 21

Example 2 :

Multiply.

(a + b)(2a² - 5ab + 3b²)

Answer :

=  (a + b)(2a² - 5ab + 3b²)

Distributive. 

=  a(2a² - 5ab + 3b²) + b(2a² - 5ab + 3b²)

Distribute again. 

=  a(2a²) + a(-5ab) + a(3b²) + b(2a²) + b(-5ab) + b(3b²)

Simplify. 

=  2a³ - 5a²b + 3ab² + 2a² b - 5ab² + 3b³

Combine the like terms.

 =  2a³ - 5a²b + 2a² b - 5ab² + 3ab²+ 3b³

 =  2a³ - 3a²b - 2ab² + 3b³

Example 3 :

Multiply.

(2x + 3y)(x² - xy + y²)

Answer :

=  (2x + 3y)(x² - xy + y²)

Distribute. 

=  2x(x² - xy + y²) + 3y(x² - xy + y²)

Distribute again.

=  2x(x²) +2x(-xy) + 2x(y²) + 3y(x²) + 3y(-xy) + 3y(y²)

Simplify. 

=  2x³ - 2x²y + 2xy² + 3x²y - 3xy² + 3y³

Combine the like terms.

 =  2x³ + x²y - xy² + 3y³

Example 4 :

Multiply.

(m - n)(m² + mn + n²)

Answer :

=  (m - n)(m² + mn + n²)

Distribute.

=  m(m² + mn + n²) - n(m² + mn + n²)

Distribute again. 

=  m(m²) + m(mn) + m(n²) - n(m²) - n(mn) - n(n²)

=  m³ + m²n + mn² - m²n - mn² - n³

Combine the like terms.

=  m³ - n³

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.