MULTIPLYING A POLYNOMIAL BY A MONOMIAL

Using distributive property of multiplication, you can multiply a polynomial (a + b + c) by a monomial (a) as shown below.   

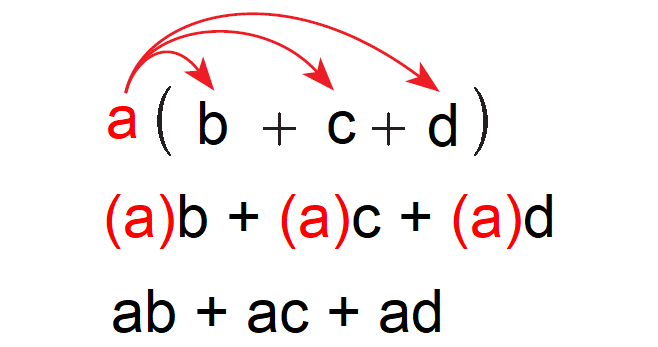
Example 1 : 

Multiply. 

2(3x² + 5x + 7)

Solution : 

=  2(3x² + 5x + 7)

Distribute 2.

=  2(3x²) + 2(5x) + 2(7)

Multiply. 

=  6x² + 10x + 14

Example 2 : 

Multiply. 

-5(2x³ - 5x² + 7x - 3)

Solution : 

=  -5(2x³ - 5x² + 7x - 3)

Distribute -5.

=  -5(2x³) - 5(-5x²) - 5(7x) - 5(-3)

Multiply. 

=  -10x³ + 25x² - 35x + 15 

Example 3 : 

Multiply. 

2x²y(4x - y)

Solution : 

=  2x²y(4x - 3y)

Distribute 2x²y.

=  2x²y(4x) + 2x²y(-3y)

Group like terms together. 

=  (2 ⋅ 4)(x² ⋅ x)(y) + 2(-3)(x²)(y ⋅ y)

Use the Product of Powers Property. 

=  8x^{2 + 1}y - 6x²y^{1 + 1}

=  8x³y - 6x²y²

Example 4 : 

Multiply. 

5a(a²b + 3b²)

Solution : 

=  5a(a²b + 3b²)

Distribute 5a.

=  5a(a²b) + 5a(3b²)

Group like terms together. 

=  5(a ⋅ a²)b + (5 ⋅ 3)ab²

Use the Product of Powers Property. 

=  5a^{1 + 2}b + 15ab²

=  5a³b + 15ab²

Example 5 : 

Multiply. 

3ab(5a² + b)

Solution : 

=  3ab(5a² + b)

Distribute 3ab.

=  3ab(5a²) + 3ab(b)

Group like terms together. 

=  (3 ⋅ 5)(a ⋅ a²)b + 3a(b ⋅ b)

Use the Product of Powers Property. 

=  15a^{1 + 2}b + 3ab^{1 + 1}

=  15a³b + 3ab²

Example 6 : 

Multiply. 

-2a²b³(3ab² - a²b)

Solution : 

=  -2a²b³(3ab² - a²b)

Distribute -2a²b³.

=  -2a²b³(3ab²) - 2a²b³(-a²b)

Group like terms together. 

=  -(2 ⋅ 3)(a² ⋅ a)(b³ ⋅ b²) - (2 ⋅ -1)(a² ⋅ a²)(b³ ⋅ b)

Use the Product of Powers Property. 

=  -6a^{2 + 1}b^{3 + 2} - (-2)a^{2 + 2}b^{3 + 1}

=  -6a³b⁵ + 2a⁴b⁴

Example 7 : 

Multiply. 

2xy(x²y + xz - xy)

Solution : 

=  2xy(x²y + xz - xy)

Distribute 2xy.

=  2xy(x²y) + 2xy(xz) + 2xy(-xy)

Group like terms together. 

=  2(x ⋅ x²)(y ⋅ y) + 2(x ⋅ x)yz + 2(-1)(x ⋅ x)(y ⋅ y)

Use the Product of Powers Property. 

=  2x^{1 + 2}y^{1 + 1} + 2x^{1 + 1}yz - 2x^{1 + 1}y^{1 + 1}

=  2x³y² + 2x²yz - 2x²y²

Example 8 : 

Multiply. 

2a²b(ab² - a²b + ab)

Solution : 

=  2a²b(ab² - a²b + ab)

Distribute 2a²b.

=  2a²b(ab²) + 2a²b(-a²b) + 2a²b(ab)

Group like terms together. 

=  2(a² ⋅ a)(b ⋅ b²) + (2 ⋅ -1)(a² ⋅ a²)(b ⋅ b) + 2(a² ⋅ a)(b ⋅ b)

Use the Product of Powers Property. 

=  2a^{2 + 1}b^{1 + 2} - 2a^{2 + 2}b^{1 + 1} + 2a^{2 + 1}b^{1 + 1}

=  2a³b³ - 2a⁴b² + 2a³b²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.