MULTIPLYING POLYNOMIALS WORKSHEET

1) Multiply the following polynomials and find the degree of the resultant polynomial:

(i)  p(x)  =  x² - 9 and q(x)  =  6x² + 7x - 2

(ii)  f(x)  =  7x + 2 and g(x)  =  15x - 9 

(iii)  h(x)  =  6x² - 7x + 1 and f(x)  =  5x - 7

2) The cost of a chocolate is Rs. (x + y) and Amir bought (x + y) chocolates. Find the total amount paid by him in terms of x and y. If x = 10, y = 5 find the amount paid by him.

3) The length of a rectangle is (3x+2) units and it’s breadth is (3x–2) units. Find its area in terms of x. What will be the area if x = 20 units. 

4) p(x) his a polynomial of degree 1 and q(x) is a polynomial of degree 2. What kind of the polynomial p(x) × q(x) is ?

Detailed Answer Key

Answer (1)(i) :

p(x) ⋅ q(x)  =  (x² - 9)(6x² + 7x - 2)

  =  6x⁴ + 7x³ - 56x² - 63x + 18

Degree of the resultant polynomial is 4.

Answer (1)(ii) : 

f(x) ⋅ g(x)  =  (7x + 2)(15x - 9) 

  =  105x² - 33x - 18

Degree of the resultant polynomial is 2.

Answer (1)(iii) :

h(x) ⋅ f(x)  =  (6x² - 7x + 1)(5x - 7)

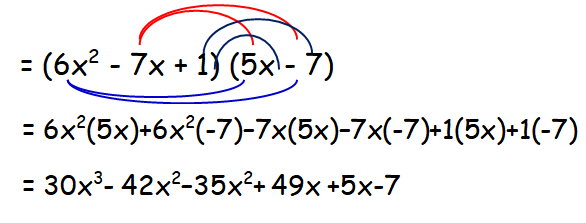
=  30x³ - 77x² + 54x - 7

Degree of the resultant polynomial is 3.

Answer (2) :

In order to find the total amount paid by him, we have to multiply the cost of 1 chocolate by the number of chocolate he buys.

Cost of 1 chocolate  =  x + y

Number of chocolates he buys  =  x + y

Total amount  =  (x + y) (x + y)

  =  (x + y)²  ---(1)

  =  x² + 2xy + y²

By applying the values of x and y, we get 

  =  (10 + 5)²

  =  15²

  =  225

Hence he has to pay Rs. 225.

Answer (3) :

Length of the rectangle  =  3x + 2

Breadth of the rectangle  =  3x - 2

Area of rectangle  =  (3x + 2)(3x - 2)

  =  9x² - 6x + 6x - 4

  =  9x² - 4

If x = 20

Area of rectangle  =  9(20)² - 4

  =  9(400) - 4

  =  3600 - 4

  =  3596

Answer (4) :

The degree of the polynomial p(x) is 1

Degree of the polynomial q(x) is 2.

The product of polynomial is 3.

Hence it is a cubic polynomial.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.