MULTIPLYING POLYNOMIALS

Multiplying Monomials

Product of powers property can be used to find the product of monomials. 

Product of Powers Property :

The product of two powers with the same base equals that base raised to the sum of the exponents. 

If x is any nonzero real number and m and n are integers, then

x^m ⋅ xⁿ  =  x^m+n

Example 1 :

Multiply. 

(4y²)(5y³)

Solution :

=  (4y²)(5y³)

Group factors with like bases together. 

=  (4 ⋅ 5)(y² ⋅ y³)

Use the Product of Powers Property. 

=  20y^{2 + 3}

=  20y⁵

Example 2 :

Find the product of the following monomials.

xyz and x²yz

Solution :

=  xyz ⋅  x²yz

Group factors with like bases together. 

=  (x ⋅ x²)(y ⋅ y)(z ⋅ z)

Use the Product of Powers Property. 

=  (x^{1 + 2})(y^{1 + 1})(z^{1 + 1})

=  (x³)(y²)(z²)

=  x³y²z²

Multiplying Binomials

You can use the following methods to multiply a binomial by a binomial.

(i) Distributive Property.

(ii) FOIL Method

To multiply a binomial by a binomial, Distributive Property can be used more than once.  

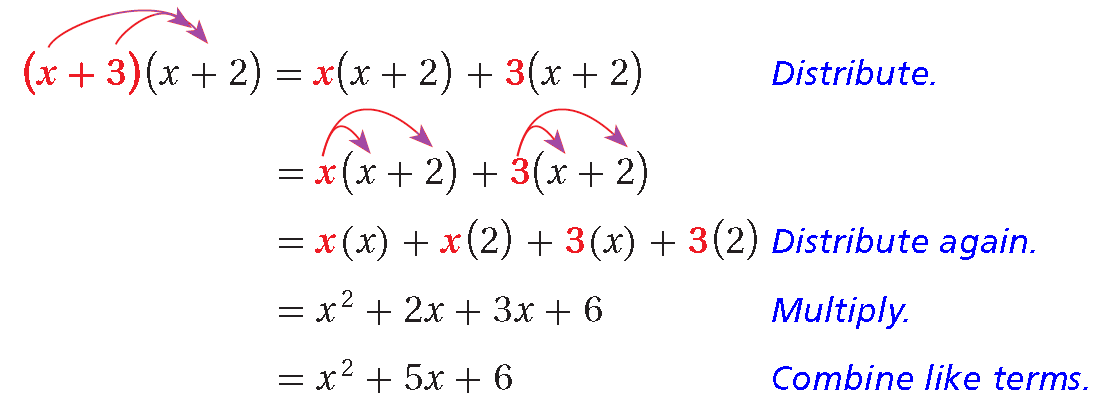
Another method for multiplying binomials is called the FOIL method. 

1. Multiply the First terms.

2. Multiply the Outer terms.

3. Multiply the Inner terms.

4. Multiply the Last terms.

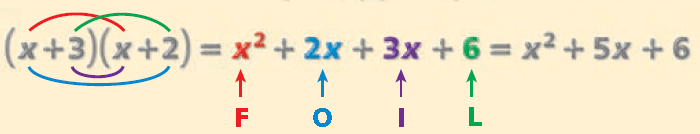
Example 1 : 

Multiply. 

(x + 3)(x - 6)

Solution : 

=  (x + 3)(x - 6)

Distribute. 

=  x(x - 6) + 3(x - 6)

Distribute again. 

=  x(x) + x(-6) + 3(x) + 3(-6)

Multiply. 

=  x² - 6x + 3x - 18

Combine like terms. 

=  x² - 3x - 18

Example 2 : 

Multiply. 

(2x - y²)(x + 4y²)

Solution : 

=  (2x - y²)(x + 4y²)

Use the FOIL method. 

=  (2x ⋅ x) + (2x ⋅ 4y²) + (-y² ⋅ x) + (-y² ⋅ 4y²)

Multiply. 

=  2x² + 8xy² - xy² - 4y⁴

Combine like terms. 

=  2x² - 7xy² - 4y⁴

Multiplying a Polynomial by a Monomial

Using distributive property of multiplication, you can multiply a polynomial (a + b + c) by a monomial (a) as shown below.   

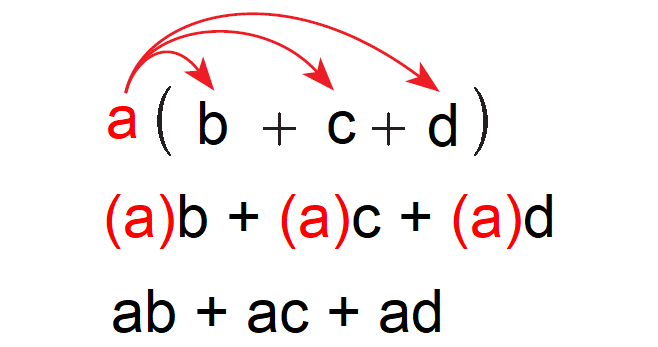
Example 1 : 

Multiply. 

2(3x² + 5x + 7)

Solution : 

=  2(3x² + 5x + 7)

Distribute 2.

=  2(3x²) + 2(5x) + 2(7)

Multiply. 

=  6x² + 10x + 14

Example 2 : 

Multiply. 

2a²b(ab² - a²b + ab)

Solution : 

=  2a²b(ab² - a²b + ab)

Distribute 2a²b.

=  2a²b(ab²) + 2a²b(-a²b) + 2a²b(ab)

Group like terms together. 

=  2(a² ⋅ a)(b ⋅ b²) + (2 ⋅ -1)(a² ⋅ a²)(b ⋅ b) + 2(a² ⋅ a)(b ⋅ b)

Use the Product of Powers Property. 

=  2a^{2 + 1}b^{1 + 2} - 2a^{2 + 2}b^{1 + 1} + 2a^{2 + 1}b^{1 + 1}

=  2a³b³ - 2a⁴b² + 2a³b²

Multiplying a Binomial by a Trinomial

To multiply a binomial by a trinomial, you can use the Distributive Property several times. 

Multiply (5x + 3) by (2x² + 10x - 6).

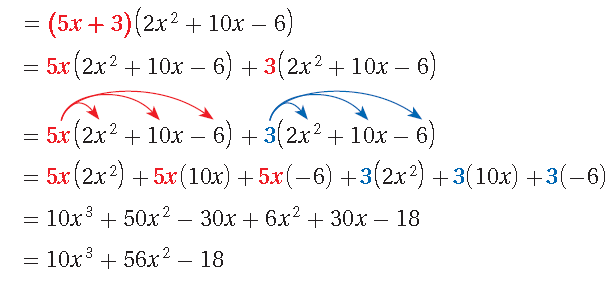
You can also use a rectangle model to multiply a binomial by a trinomial. This is similar to finding the area of a rectangle with length (2x² + 10x - 6) and width (5x + 3).

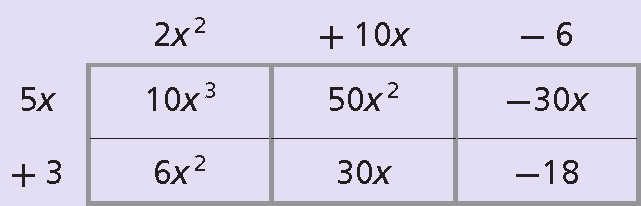
Product of monomials are written in each row and column. 

To find the product, add all of the terms inside the rectangle by combining like terms and simplifying, if necessary.   

=  10x³ + 6x² + 50x² + 30x - 30x - 18

=  10x³ + 56x² - 18

Another method that can be used to multiply a binomial by a trinomial is the vertical method. This is similar to methods used to multiply whole numbers. 

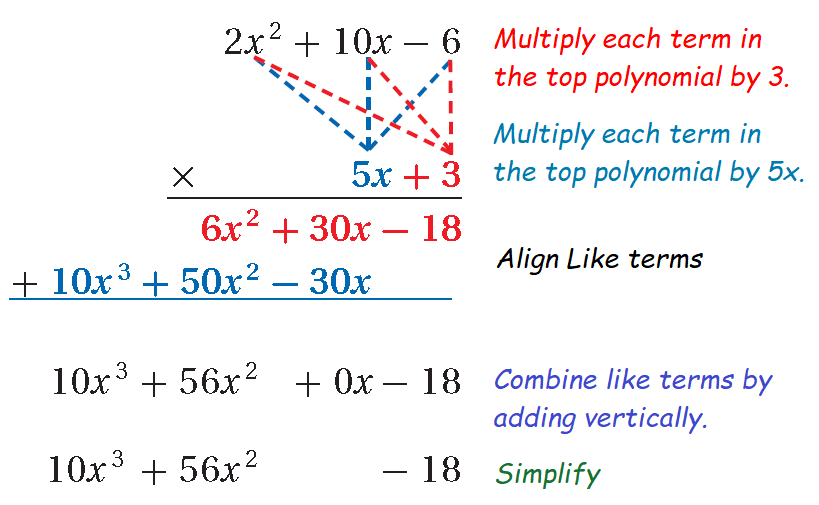
Example 1 :

Multiply.

(x + 3)(x² - 5x + 7)

Answer :

=  (x + 3)(x² - 5x + 7)

Distributive. 

=  x(x² - 5x + 7) + 3(x² - 5x + 7)

Distribute again. 

=  x(x²) + x(-5x) + x(7) + 3(x²) + 3(-5x) + 3(7)

Simplify. 

=  x³ - 5x² + 7x + 3x² - 15x + 21

Combine the like terms.

=  x³ - 5x²  + 3x²+ 7x - 15x + 21

=  x³ - 2x² - 8x + 21

Example 2 :

Multiply.

(m - n)(m² + mn + n²)

Answer :

=  (m - n)(m² + mn + n²)

Distribute.

=  m(m² + mn + n²) - n(m² + mn + n²)

Distribute again. 

=  m(m²) + m(mn) + m(n²) - n(m²) - n(mn) - n(n²)

=  m³ + m²n + mn² - m²n - mn² - n³

Combine the like terms.

=  m³ - n³

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.