MULTIPLYING RATIONAL NUMBERS WITH THE SAME SIGN

If we want to multiply two rational numbers, first we have to multiply the signs of the numbers. 

The rules for the signs of products of rational numbers with the same sign are summarized below.

Let p and q be rational numbers.

From the above rules, it is clear that when we multiply two rational numbers with the same sign, the result is always positive. 

Example 1 : 

Multiply -16 and -1/8. 

Solution : 

Step 1 : 

In the two rational numbers -16 and -1/8, the signs are same. 

Step 2 : 

Find the product of 16 and 1/8

16 x 1/8  =  16/8  =  16/8  =  2 

Step 3 : 

Since we multiply two rational numbers with the same sign, the result is always positive. 

So,

-16 x (-1/8)  =  2

Example 2 : 

Multiply 1/6 and 3/10. 

Solution : 

Step 1 : 

In the two rational numbers 1/6 and 3/10, the signs are same. 

Step 2 : 

Find the product of 1/6 and 3/10.

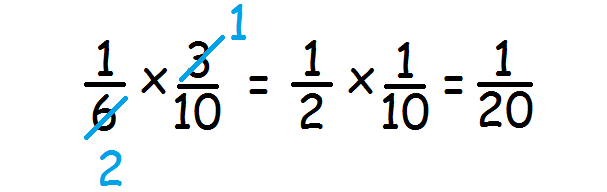
Step 3 : 

Since we multiply two rational numbers with the same sign, the result is always positive. 

So,

(1/6) x (3/10)  =  1/20

Example 3 : 

Multiply -4 and -4.5. 

Solution : 

Step 1 : 

In the two rational numbers -4 and -4.5, the signs are same. 

Step 2 : 

Find the product of 4 and 4.5

4 x 4.5  =  18 

Step 3 : 

Since we multiply two rational numbers with the same sign, the result is always positive. 

So,

-4 x (-4.5)  =  18

Example 4 : 

Multiply -2 and -3.5 using number line. 

Solution : 

Step 1 : 

First find the product -2(-3.5)

Step 2 :

On the number line, start at 0 and move 3.5 units to the left two times.   

Step 3 : 

The result is -7.

Step 4 :

This shows that 2 groups of -3.5 equals -7. So, -2 groups of -3.5 must equal the opposite of -7.

Step 5 :

-2(-3.5) =  7    A negative times a negative equals a  the the the the the the positive.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.