ONLINE FREE MATH WORKSHEET FOR GRADE 5

Online Free Math Worksheet for Grade 5 :

In this section, we will see some practice problems for 5th grade students.

Question 1 :

An urn contains red, green and blue marbles. Keisha is told 60% of the marbles are blue and that the bag contains 23 red marbles and 33 green marbles. How many blue marbles are in the urn?

(A) 84    (B) 58    (C) 70

Solution :

Let x be the total number of marbles.

Number of blue marbles  =  60% of x

  =  3x / 5

Number of red marbles  =  23

Number of green marbles  =  33

(3x/5) + 23 + 33  =  x

(3x/5) + 56  =  x

2x/5  =  56

x  =  140

Number of blue marbles  =  60% of 140

  =  0.60 (140)

  =  84

Hence 84 marbles are blue.

Question 2 :

How many numbers are divisible by 7 between 10 and 50 ?

(A) 7     (B) 5     (C) 6

Solution :

After 10, 14 is the first number which is divisible by 7

14, 21, 28, ........49

The sequence is an arithmetic progression. To find the total number of terms, we may use the formula

n  =  [(l - a)/d]  + 1

n  =  [(49 - 14)/7] + 1

n  =  (35/7) + 1

n  =  6

Question 3 :

The number of perfect squares between 10 and 103 is

(A) 2     (B) 5     (C) 7

Solution :

4²  =  16

5²  =  25

...........

.............

10²  =  100

11²  =  121 > 103

So, there are 7 perfect squares between 10 and 103.

Question 4 :

Mark bought two types of plants at a nursery for his garden. Each plant of first type cost $3 and each plant of second type cost $4. If he had spent exactly $18 to buy both the types, how many plants of first type would he have bought ?

(A) 1     (B) 2     (C) 5

Solution :

Let x and y be the number of plants in first type and second type respectively.

3x + 4y  =  18

4y  =  18 - 3x

y  =  (18 - 3x)/4

If x  =  2, then y  =  (18 - 6)/4

y  =  12/4

y  =  3

So he have bought 2 plants in first type.

Question 5 :

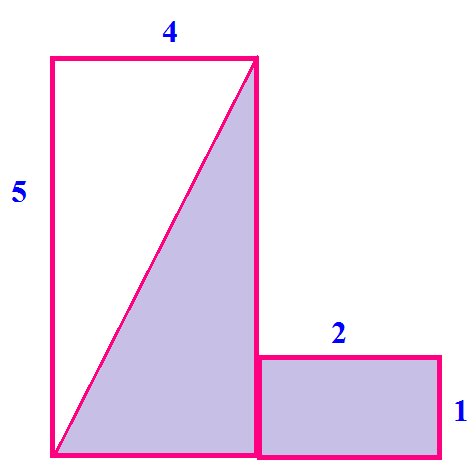
The area of the shaded portion in the above figure

(A)  15     (B)  28      (C)  12

Solution :

Here we have two shapes, a triangle and a rectangle.

Area of triangle  =  (1/2)⋅b⋅h

  =  (1/2) ⋅ 4 ⋅ 5

  =  10

Area of rectangle  =  l ⋅ w

  =  2 ⋅ 1

  =  2

Area of shaded region  =  10 + 2

  =  12

Question 6 :

Find the greatest common factor of 24 and 30?

(A) 4      (B) 5     (C) 6

Solution :

Factors of 24 are,

1, 2, 3, 4, 6, 8, 12, 24  

Factors of 30 are,

1, 2, 3, 5, 6, 15, 30

Hence the greatest common factor is 6.

Question 7 :

The value of 5 cubed times 2 squared is

(A) 570     (B) 250      (C) 500

Solution :

5³ + 2²  =   125 + 8

=  133

Question 8 :

In how many ways, Can five people stand in a line for a photograph?

(A) 120     (B) 152      (C) 520

Solution :

First person having 5 places to stand. Second person will have 4 options.

Like that the number of options be 

=  5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1

=  120

Hence the number of ways are 120.

Question 9 :

Michael and David went on a three day hike. They hiked 10 miles per day. The first day they took 3 hours of hiking to travel 10 miles. On the second day they took 5 hours. If the average rate of speed for the entire trip was 2.5 miles per hour, how many hours of hiking did they take to travel 10 miles on the third day?

(A) 4      (B) 2      (C) 5

Solution :

Average speed  =  Total distance covered / Total time taken

2.5  =  (10 + 10 + 10) / (3 + 5 + T)

  2.5  =  30 / (8 + T)

  8 + T  =  30/2.5

8 + T  =  12

T  =  12 - 8

T  =  4

Question 10  :

The value of 25! / 24! factorial is

(A) 18    (B) 25     (C) 30

Solution :

25! / 24!  =  25 (24!)/24!

  =  25

After having gone through the stuff given above, we hope that the students would have practiced problems in the worksheet.

Apart from the stuff given on this web page, if you need any other stuff in math, please use our google custom search here

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.