OPERATIONS WITH RATIONAL NUMBERS PROBLEMS 

Problem 1 :

Fill in the blanks

(i)  The multiplicative inverse of 2  3/5 is  _______

Solution :

For any non-zero rational number b there exists a unique rational number 1/b such that b x (1/b) =  1  =  (1/b) × b (Multiplicative Inverse property).

First let us convert the mixed fraction into improper fraction.

2  3/5  =  (10 + 3)/5  =  13/5

The multiplicative inverse of 13/5 is 5/13.

(ii) If −3 ⋅ (6/-11)  =  (6/-11) ⋅ x, then x is ________.

Solution :

In order to get same answer for both left hand side and right hand side, we have to remember the commutative law.

a x b  =  b x a

So, the value of x is -3.

(iii) If distributive property is true for

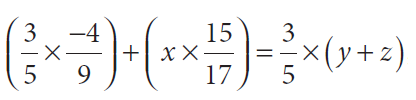
then x, y, z are ________ , ________ and ________.

Solution :

R.H.S :

  =  (3/5) (y + z)

  =  (3/5) ⋅ y + (3/5) ⋅ z   ------(1)

L.H.S :

(3/5) ⋅ (-4/9) + (x ⋅ (15/17))   ------(2)

(1)  =  (2)

 (3/5) ⋅ (-4/9) + (x ⋅ (15/17))  =  (3/5) ⋅ y + (3/5) ⋅ z  

x  =  3/5, y  =  -4/9 and z  =  15/17

(iv) If x ⋅ (-55/63)  =  (-55/63) ⋅  x  =  1, then x is called the _________________ of 55/63 . 

Solution :

Since the product of x and -55/63 is 1, we say that x is the multiplicative inverse of -55/63.

Hence the value of x is -63/55.

(v) The multiplicative inverse of -1 is ________.

Solution :

The multiplicative inverse of -1 is -1.

Problem 2 :

Say True or False:

(i)  (−7/8) × (−23/27)  = (−23/27) × (−7/8) illustrates the closure property of rational numbers.

Solution :

The given statement exactly matches with the general form

 a x b  =  b x a

It means commutative property not closure.

Hence the answer is False.

(ii)  Associative property is not true for subtraction of rational numbers.

Solution :

(a - b) - c  =  a - (b - c)

If associative property is true, then it satisfies the above statement.

Let a = 1/2, b = 1/3 and c = 5/6

(a - b) - c  =  [(1/2) - (1/3)] - 5/6

  =  (1/6) - (5/6)

  =  (1-5)/6

  =  -4/6

  =  -2/3 -----(1)

a - (b - c)  =  (1/2) - [(1/3)- 5/6]

  =  (1/2) - (-3/6)

  =  (3 + 3)/6

  =  1 -----(2)

Hence the answer is True.

(iii)  The additive inverse of −11/(-17) is 11/17.

Solution :

The answer is false.

By simplifying 11/17 and 11/17, we will not get 0.

(iv) The product of two negative rational numbers is a positive rational number

Solution :

The answer is True. Because negative times negative is positive.

(v) The multiplicative inverse exists for all rational numbers.

Solution :

For the rational number 0 there is no multiplicative inverse. Hence the answer is false.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.