ORDER OF ROTATIONAL SYMMETRY WORKSHEET
1. What is the order of rotational symmetry of an equilateral triangle?
2. What is the order of rotational symmetry of a square?
3. What is the order of rotational symmetry of a regular pentagon?
4. What is the order of rotational symmetry of a parallelogram?
5. What is the order of rotational symmetry of an isosceles triangle?
6. What is the order of rotational symmetry of a scalene triangle?
7. What is the order of rotational symmetry of a trapezium?
8. What is the order of rotational symmetry of an isosceles trapezium?
9. What is the order of rotational symmetry of a kite?
10. What is the order of rotational symmetry of a rhombus?
11. What is the order of rotational symmetry of an ellipse?
12. What is the order of rotational symmetry of a circle?

Answers
1. Answer :
By definition, we have to check how many times an equilateral triangle fits on to itself during a full rotation of 360 degrees.
Please look at the images of the equilateral triangle in the order A,B and C. A is the original image. The images B and C are generated by rotating the original image A.
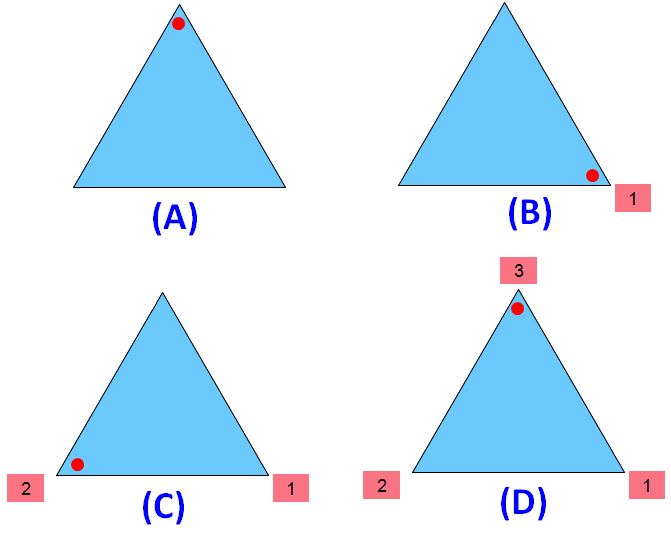
When we look at the above images of equilateral triangle, it fits on to itself 3 times during a full rotation of 360 degrees.
So, an equilateral triangle has rotational symmetry of order 3.
2. Answer :
Please look at the images of the square in the order A, B, C, D and E. A is the original image. The images B, C, D and E are generated by rotating the original image A.
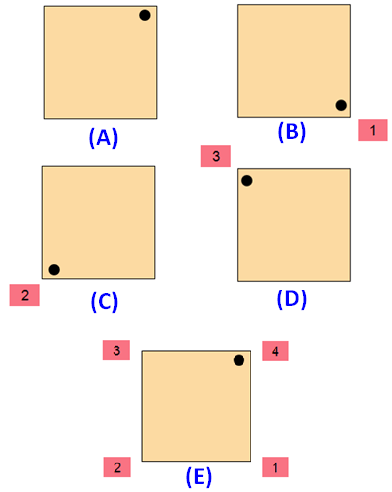
When we look at the above images of square, it fits on to itself 4 times during a full rotation of 360 degrees.
So, a square has rotational symmetry of order 4.
3. Answer :
Please look at the images of the regular pentagon in the order A, B, C, D, E and F. A is the original image. The images B, C, D, E and F are generated by rotating the original image A.
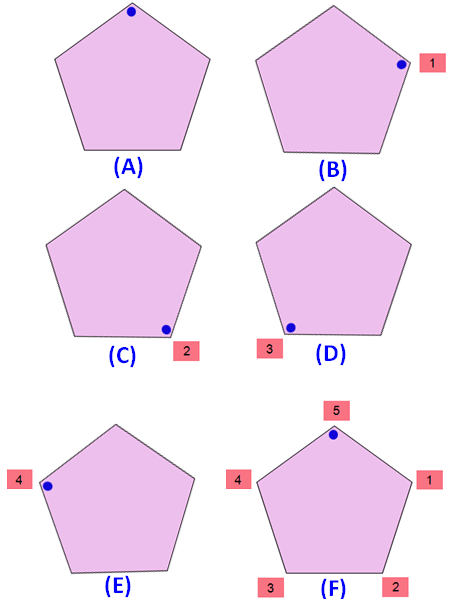
When we look at the above images of regular pentagon, it fits on to itself 5 times during a full rotation of 360 degrees.
So, a regular pentagon has rotational symmetry of order 5.
4. Answer :
Please look at the images of the parallelogram in the order A, B and C. A is the original image. The images B and C are generated by rotating the original image A.
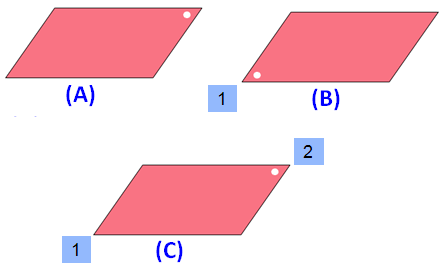
When we look at the above images of parallelogram, it fits on to itself 2 times during a full rotation of 360 degrees.
So, a parallelogram has rotational symmetry of order 2.
5. Answer :
Please look at the images of the isosceles triangle in the order A and B. A is the original image. The image B is generated by rotating the original image A.
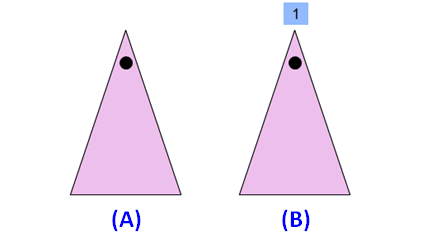
When we look at the above images of isosceles triangle, it fits on to itself 1 time during a full rotation of 360 degrees.
So, an isosceles triangle has rotational symmetry of order 1.
6. Answer :
Please look at the images of the scalene triangle in the order A and B. A is the original image. The image B is generated by rotating the original image A.
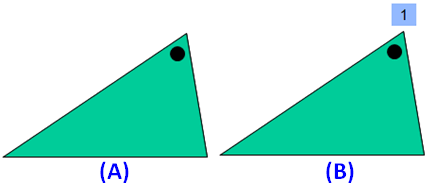
When we look at the above images of isosceles triangle, it fits on to itself 1 time during a full rotation of 360 degrees.
So, a scalene triangle has rotational symmetry of order 1.
7. Answer :
Please look at the images of the trapezium in the order A and B. A is the original image. The image B is generated by rotating the original image A.
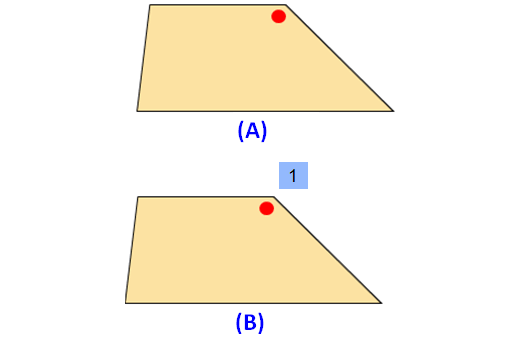
When we look at the above images of trapezium, it fits on to itself 1 time during a full rotation of 360 degrees.
So, a trapezium has rotational symmetry of order 1.
8. Answer :
Please look at the images of the isosceles trapezium in the order A and B. A is the original image. The image B is generated by rotating the original image A.
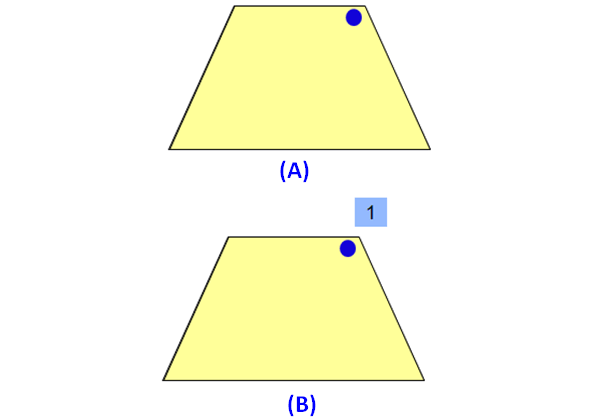
When we look at the above images of isosceles trapezium, it fits on to itself 1 time during a full rotation of 360 degrees.
So, an isosceles trapezium has rotational symmetry of order 1.
9. Answer :
Please look at the images of the kite in the order A and B. A is the original image. The image B is generated by rotating the original image A.
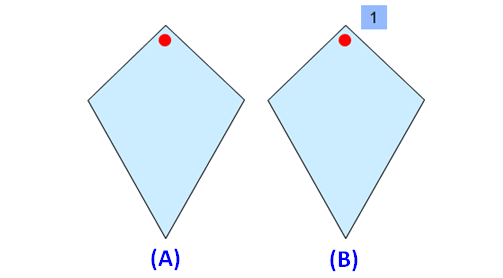
When we look at the above images of kite, it fits on to itself 1 time during a full rotation of 360 degrees.
So, a kite has rotational symmetry of order 1.
10. Answer :
Please look at the images of the rhombus in the order A, B and C. A is the original image. The images B and C are generated by rotating the original image A.
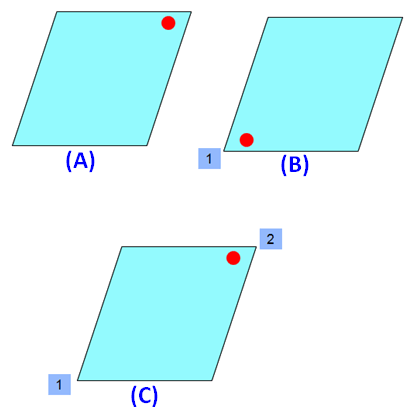
When we look at the above images of rhombus, it fits on to itself 2 time during a full rotation of 360 degrees.
So, a rhombus has rotational symmetry of order 2.
11. Answer :
Please look at the images of the ellipse in the order A, B and C. A is the original image. The images B and C are generated by rotating the original image A.
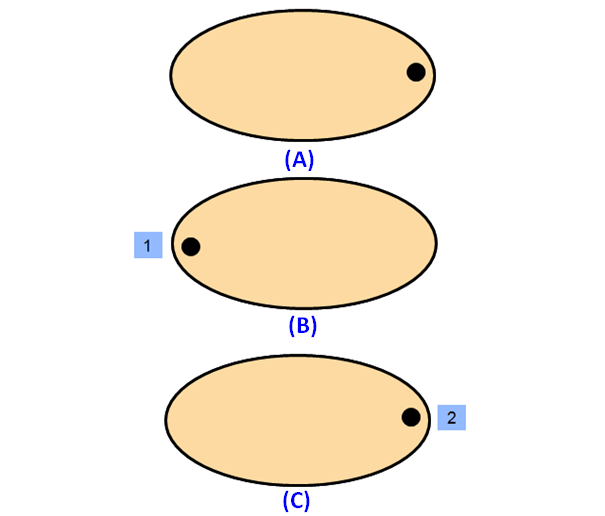
When we look at the above images of ellipse, it fits on to itself 2 time during a full rotation of 360 degrees.
So, an ellipse has rotational symmetry of order 2.
11. Answer :
A circle has an infinite 'order of rotational symmetry'. In simplistic terms, a circle will always fit into its original outline, regardless of how many times it is rotated.
Hence, a circle has infinite order of rotational symmetry.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
AP Calculus AB Problems with Solutions (Part - 19)
Apr 24, 25 11:10 PM
AP Calculus AB Problems with Solutions (Part - 19) -
AP Calculus AB Problems with Solutions (Part - 18)
Apr 24, 25 11:06 PM
AP Calculus AB Problems with Solutions (Part - 18) -
Derivative of Absolute Value of x Using Limit Definition
Apr 23, 25 11:11 AM
Derivative of Absolute Value of x Using Limit Definition
