ORDERING REAL NUMBERS WORKSHEET

Question 1 : 

Order √22, π + 1 and 4 1/2 from least to greatest. Then graph them on the number line.

Question 2 : 

Order 4√2, 2√3, 3√2, √17, 3√3 and 5 from least to greatest.

Detailed Answer Key

Question 1 : 

Order √22, π + 1 and 4 1/2 from least to greatest. Then graph them on the number line.

Answer : 

Step 1 :

First approximate √22.

√22 is between 4 and 5. Since we don’t know where it falls between 4 and 5, we need to find a better estimate for √22. 

So that we can compare it to 4 1/2.

Since 22 is closer to 25 than 16, use squares of numbers between 4.5 and 5 to find a better estimate of √22. 

4.5²  =  20.25

4.6²  =  21.16

4.7²  =  22.09

4.8²  =  23.04

Since 4.7²  =  22.09, an approximate value for  √22 is 4.7.

That is, 

√22  ≈  4.7 -----(1)

Step 2 :

An approximate value of π is 3.14. So an approximate value of π+1 is 4.14.

That is, 

π + 1  ≈  4.14 -----(2)

Step 3 :

The value of 4 1/2 is 4.5. 

That is, 

4 1/2  =  4.5 -----(3)

Step 4 :

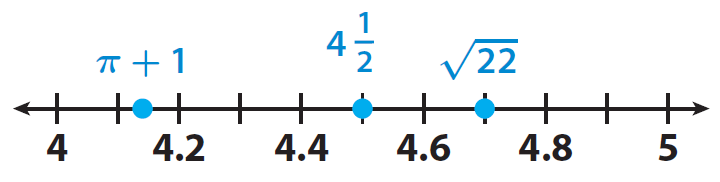
Comparing (1), (2) and (3), we can order the numbers from least to greatest as given below. 

π + 1, 4 1/2 and √22

Step 5 :

Read the numbers from left to right to place them on a number line in order from least to greatest.

Question 2 : 

Order 4√2, 2√3, 3√2, √17, 3√3 and 5 from least to greatest.

Answer :

Key Concept :

Most of the given numbers are irrational numbers.

So, square the given numbers and order them from least to greatest.

Step 1 :

Take square to 4√2. 

(4√2)²  =  (4)²(√2)²

(4√2)²  =  (16)(2)

(4√2)²  =  32 -----(1)

Step 2 :

Take square to 2√3. 

(2√3)²  =  (2)²(√3)²

(2√3)²  =  (4)(3)

(2√3)²  =  12 -----(2)

Step 3 :

Take square to 3√2. 

(3√2)²  =  (3)²(√2)²

(3√2)²  =  (9)(2)

(3√2)²  =  18 -----(3)

Step 4 :

Take square to √17. 

(√17)²  =  17 -----(4)

Step 5 :

Take square to 3√3. 

(3√3)²  =  (3)²(√3)²

(3√3)²  =  (9)(3)

(3√3)²  =  27 -----(5)

Step 6 :

Take square to 5. 

(5)²  =  25 -----(6)

Step 7 :

Comparing (1), (2), (3), (4), (5) and (6), we can write the squares of the given irrational numbers from least to greatest as given below. 

12, 17, 18, 25, 27, 32

In the above order, write the corresponding real number to its square to write the given real numbers in the order from least to greatest. 

2√3, √17, 3√2, 5, 3√3, 4√2

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.