OVERLAPPING ARCS WORKSHEET

Problem 1 :

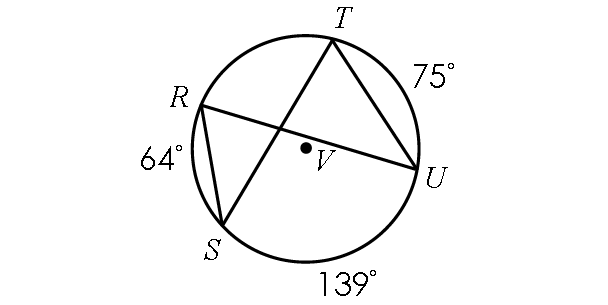
Find m∠RST and m∠RUT. 

Problem 2 : 

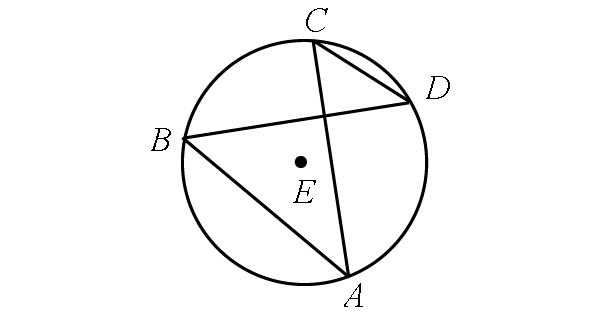
If m∠ABD = (6x + 26)° and m∠ACD = (13x - 9)°, find m∠arc AD. 

Problem 3 : 

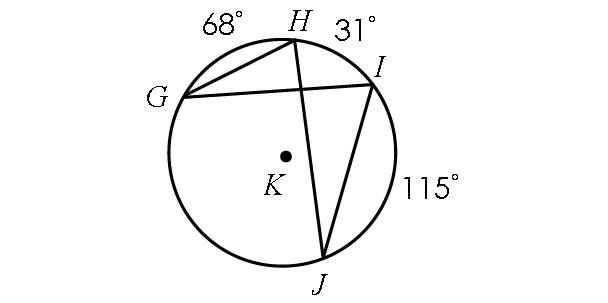
Find m∠GHJ and m∠GIJ. 

Problem 4 : 

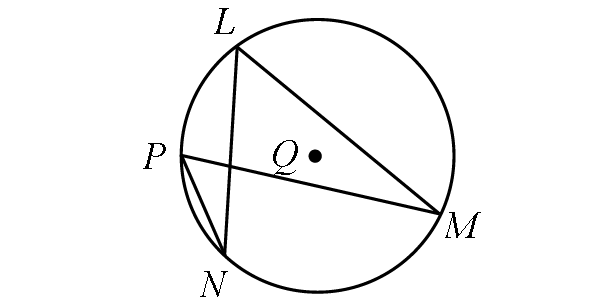
If m∠LMP = (5x - 19)° and m∠LNP = (2x + 11)°, find m∠arc PL. 

Problem 5 : 

Find m∠arc WX. 

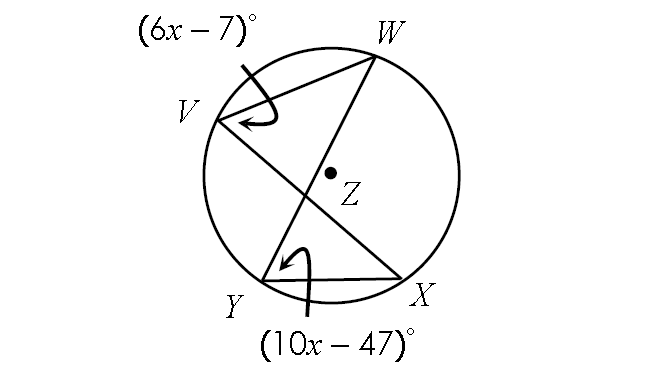
Problem 6 : 

In circle P, if m∠arc QR = 110°, m∠arc RS = 94° and m∠QRT = 27°, find the following measures : 

(i) m∠QTR, (ii) m∠QSR, (iii) m∠arc QT,

(iv) m∠arc TS, (v) m∠TRS, (vi) m∠RQS

Detailed Answer Key

Problem 1 :

Find m∠RST and m∠RUT. 

Solution : 

In the diagram above, 

m∠arc RT + m∠arc TU + m∠arc US + m∠arc SR  =  360°

m∠arc RT + 75° + 139° + 64°  =  360°

m∠arc RT + 75° + 139° + 64°  =  360°

m∠arc RT + 278°  =  360°

Subtract 278° from each side. 

m∠arc RT  =  82°

By Inscribed Angle Theorem, 

m∠RST  =  1/2 ⋅ m∠arc RT

m∠RST  =  1/2 ⋅ 82°

m∠RST  =  41°

In the diagram above, two inscribed angles m∠RST and m∠RUT intercept the same arc RT. So, the angles are congruent. 

m∠RUT  =  m∠RST

m∠RUT  =  41°

Problem 2 : 

If m∠ABD = (6x + 26)° and m∠ACD = (13x - 9)°, find m∠arc AD. 

Solution :

In the diagram above, two inscribed angles m∠ABD and m∠ACD intercept the same arc AD. So, the angles are congruent. 

m∠ABD  =  m∠ACD

(6x + 26)°  =  (13x - 9)°

6x + 26  =  13x - 9

Subtract 6x from each side. 

26  =  7x - 9

Add 9 to each side. 

35  =  7x

Divide each side by 7.

5  =  x

Finding m∠ABD. 

m∠ABD  =  (6x + 26)°

Substitute x = 5. 

m∠ABD  =  [6(5) + 26]°

m∠ABD  =  [30 + 26]°

m∠ABD  =  56°

By Inscribed Angle Theorem, 

m∠arc AD  =  2 ⋅ m∠ABD

m∠arc AD  =  2 ⋅ 56°

m∠arc AD  =  112°

Problem 3 : 

Find m∠GHJ and m∠GIJ. 

Solution :

In the diagram above, 

m∠arc GJ + m∠arc JI + m∠arc IH + m∠arc HG  =  360°

m∠arc GJ + 115° + 31° + 68°  =  360°

m∠arc GJ + 214°  =  360°

Subtract 214° from each side. 

m∠arc GJ  =  146°

By Inscribed Angle Theorem, 

m∠GHJ  =  1/2 ⋅ m∠arc GJ

m∠GHJ  =  1/2 ⋅ 146°

m∠GHJ  =  73°

In the diagram above, two inscribed angles m∠GHJ and m∠GIJ intercept the same arc GJ. So, the angles are congruent. 

m∠GIJ  =  m∠GHJ

m∠GIJ  =  73°

Problem 4 : 

If m∠LMP = (5x - 19)° and m∠LNP = (2x + 11)°, find m∠arc PL. 

Solution :

In the diagram above, two inscribed angles m∠LMP and m∠LNP intercept the same arc LP. So, the angles are congruent. 

m∠LMP  =  m∠LNP

(5x - 19)°  =  (2x + 11)°

5x - 19  =  2x + 11

Subtract 2x from each side. 

3x - 19  =  11

Add 19 to each side. 

3x  =  30

Divide each side by 3.

x  =  10

Finding m∠LMP. 

m∠LMP  =  (5x - 19)°

Substitute x = 10. 

m∠LMP  =  [5(10) - 19]°

m∠LMP  =  [50 - 19]°

m∠LMP  =  31°

By Inscribed Angle Theorem, 

m∠arc PL  =  2 ⋅ m∠LMP

m∠arc PL  =  2 ⋅ 31°

m∠arc PL  =  62°

Problem 5 : 

Find m∠arc WX. 

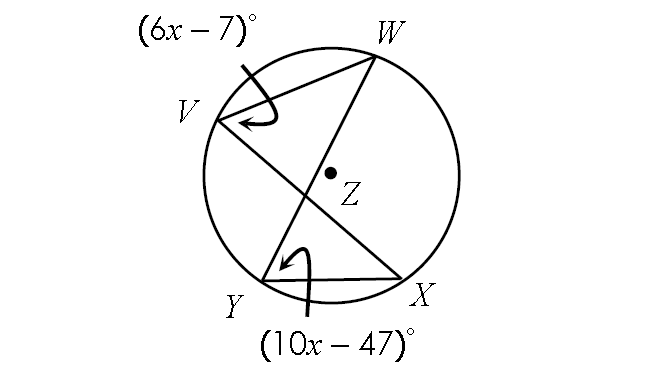
Solution :

In the diagram above, two inscribed angles m∠WVX and m∠WYX intercept the same arc WX. So, the angles are congruent. 

m∠WVX  =  m∠WYX

(6x - 7)°  =  (10x - 47)°

6x - 7  =  10x - 47

Subtract 6x from each side. 

-7  =  4x - 47

Add 47 to each side. 

40  =  4x

Divide each side by 4.

10  =  x

Finding m∠WVX.

m∠WVX  =  (6x - 7)°

Substitute x = 10.

m∠WVX  =  [6(10) - 7]°

m∠WVX  =  [60 - 7]°

m∠WVX  =  53°

By Inscribed Angle Theorem, 

m∠arc WX  =  2 ⋅ m∠WVX

m∠arc WX  =  2 ⋅ 53°

m∠arc WX  =  106°

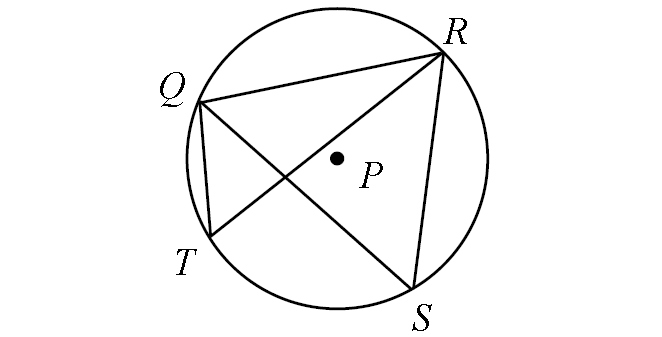
Problem 6 : 

In circle P, if m∠arc QR = 110°, m∠arc RS = 94° and m∠QRT = 27°, find the following measures : 

(i) m∠QTR, (ii) m∠QSR, (iii) m∠arc QT,

(iv) m∠arc TS, (v) m∠TRS, (vi) m∠RQS

Solution : 

(i) m∠QTR :

By Inscribed Angle Theorem, 

m∠QTR  =  1/2 ⋅ m∠arc QR

Substitute m∠arc QR = 110°.

m∠QTR  =  1/2 ⋅ 110°

m∠QTR  =  55°

(ii) m∠QSR :

In the diagram above, two inscribed angles m∠QTR and m∠QSR intercept the same arc QR. So, the angles are congruent. 

m∠QSR  =  m∠QTR

m∠QSR  =  55°

(iii) m∠arc QT :

m∠arc QT  =  2 ⋅ m∠QRT

Substitute m∠QRT = 27°.

m∠arc QT  =  2 ⋅ 27°

m∠arc QT  =  54°

(iv) m∠arc TS :

In the circle P above, 

m∠arc TS + m∠arc RS + m∠arc QR + m∠arc QT  =  360°

Substitute. 

m∠arc TS + 94° + 110° + 54°  =  360°

m∠arc TS + 258°  =  360°

Subtract 258° from each side. 

m∠arc TS  =  102°

(v) m∠TRS : 

By Inscribed Angle Theorem, 

m∠TRS  =  1/2 ⋅ m∠arc TS

Substitute m∠arc TS = 102°.

m∠TRS  =  1/2 ⋅ 102°

m∠TRS  =  51°

(vi) m∠RQS : 

By Inscribed Angle Theorem, 

m∠RQS  =  1/2 ⋅ m∠arc RS

Substitute m∠arc RS = 94°.

m∠RQS  =  1/2 ⋅ 94°

m∠RQS  =  47°

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.