PAIR OF STRAIGHT LINES QUESTIONS

Question 1 :

Prove that one of the straight lines given by ax² + 2hxy + by² = 0 will bisect the angle between the co-ordinate axes if (a + b)² = 4h²

Solution :

Given that :

(a + b)² = 4h²

Taking square roots on both sides, we get

a +  b  =  2 h

By applying the value of 2h  =  (a + b) in the given equation, we get

ax² + (a + b)xy + by² = 0

ax² + a xy + bxy + by² = 0

ax(x + y) + by(x + y)  =  0

(ax + by) (x + y)  =  0

by  =  -ax  and y  =  -x

Now let us consider the second equation y = -x.

Slope  =  -1

m = tan θ   =  -1 

θ  =  135

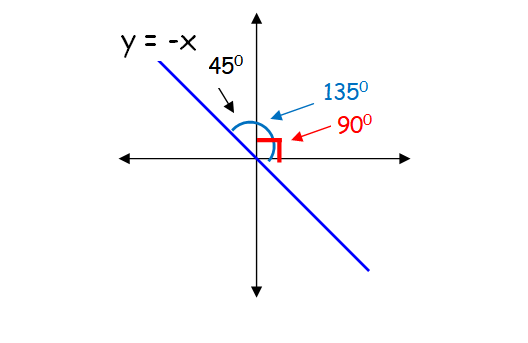
Hence proved.

Question 2 :

If the pair of straight lines x² − 2kxy − y² = 0 bisect the angle between the pair of straight lines x² − 2lxy − y² = 0, Show that the later pair also bisects the angle between the former.

Solution :

 x² − 2kxy − y² = 0

Equation of angle bisector :

x² - y²/a - b  =  xy/h

a = 1, 2h = -2k ==> h = -k, b = -1

x² - y²/(1 + 1)  =  xy/(-k)

x² - y²/2  =  -xy/k

(x² - y²) k =  -2xy

kx² + 2xy - ky²  =  0     -------(1)

 x² − 2lxy − y² = 0     -------(2)

is the equation of the bisector of the angle between the same lines(given)

From (1) and (2) by comparing the coefficients we get

k/1  =  2/(-2l)  =  -k/(-1)

k/1  =  -1/l  =  k

-1  =  kl

Question 3 :

Prove that the straight lines joining the origin to the points of intersection of 3x² + 5xy − 3y² + 2x + 3y = 0 and 3x − 2y − 1 = 0 are at right angles.

Solution :

3x − 2y  =  1

3x² + 5xy − 3y² + (2x + 3y) (1)  =  0

3x² + 5xy − 3y² + (2x + 3y) (3x − 2y)  =  0

3x² + 5xy − 3y² + (6x² - 4xy + 9xy - 6y²)  =  0

9x² + 10xy − 9y²  =  0

a  =  9 and b  =  -9

a + b  =  9 + (-9)  =  0

Hence they are perpendicular.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.