PARABOLA FORMULAS

Parabola Opens Right

Standard equation of a parabola that opens right and symmetric about x-axis with vertex at origin. 

y²  =  4ax

Standard equation of a parabola that opens up and symmetric about x-axis with at vertex (h, k). 

(y - k)²  =  4a(x - h)

Graph of y²  =  4ax :

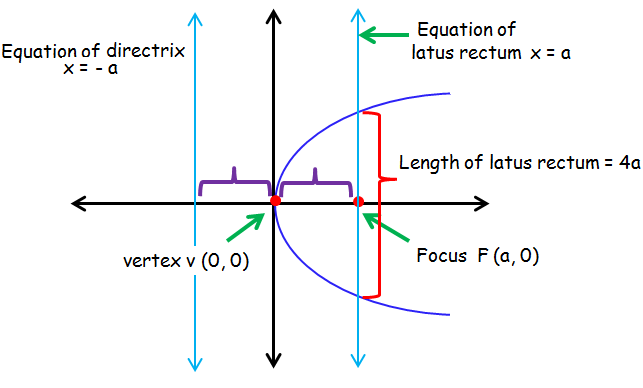
Axis of symmetry : x -axis

Equation of axis : y = 0

Vertex : V(0, 0)

Focus : F(a, 0)

Equation of latus rectum : x = a 

Equation of directrix : x = -a 

Length of latus rectum : 4a

Distance between the vertex and focus = a. 

Distance between the directrix and vertex = a. 

Distance between directrix and latus rectum = 2a.

Parabola Opens Left

Standard equation of a parabola that opens left and symmetric about x-axis with vertex at origin. 

y²  =  -4ax

Standard equation of a parabola that opens up and symmetric about x-axis with at vertex (h, k). 

(y - k)²  =  -4a(x - h)

Graph of y²  =  -4ax :

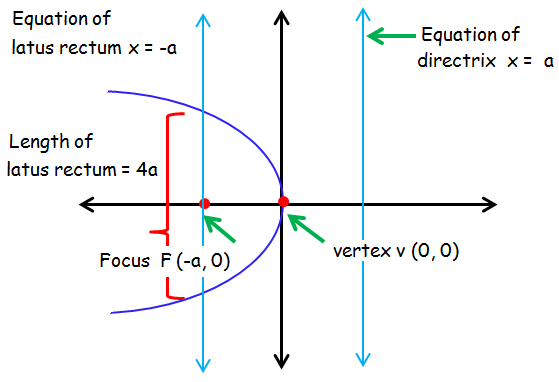
Axis of symmetry : x -axis

Equation of axis : y = 0

Vertex : V(0, 0)

Focus : F(-a, 0)

Equation of latus rectum : x = -a 

Equation of directrix : x = a 

Length of latus rectum : 4a

Distance between the vertex and focus = a. 

Distance between the directrix and vertex = a. 

Distance between directrix and latus rectum = 2a.

Parabola Opens Up

Standard equation of a parabola that opens up and symmetric about y-axis with vertex at origin. 

x²  =  4ay

Standard equation of a parabola that opens up and symmetric about y-axis with at vertex (h, k). 

(x - h)²  =  4a(y - k)

Graph of x²  =  4ay :

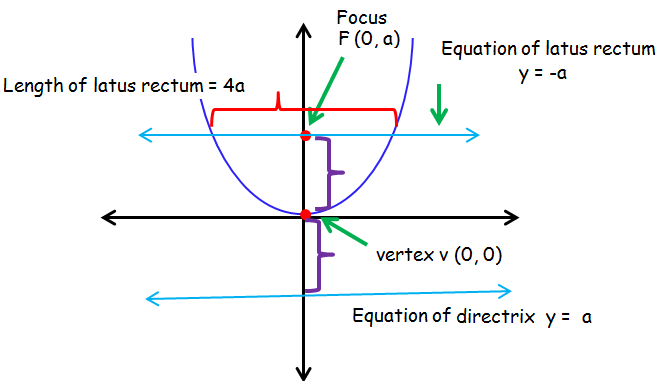
Axis of symmetry : y-axis

Equation of axis : x = 0

Vertex : V(0, 0)

Focus : F(0, a)

Equation of latus rectum : y = a 

Equation of directrix : y = -a 

Length of latus rectum : 4a

Distance between the vertex and focus = a. 

Distance between the directrix and vertex = a. 

Distance between directrix and latus rectum = 2a.

Parabola Opens Down

Standard equation of a parabola that opens up and symmetric about y-axis with vertex at origin. 

x²  =  -4ay

Standard equation of a parabola that opens up and symmetric about y-axis with at vertex (h, k). 

(x - h)²  =  -4a(y - k)

Graph of x²  =  -4ay :

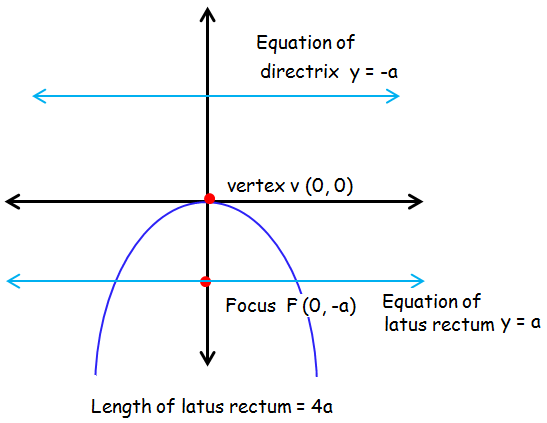
Axis of symmetry : y-axis

Equation of axis : x = 0

Vertex : V(0, 0)

Focus : F(0, -a)

Equation of latus rectum : y = -a 

Equation of directrix : y = a 

Length of latus rectum : 4a

Distance between the vertex and focus = a. 

Distance between the directrix and vertex = a. 

Distance between directrix and latus rectum = 2a.

Solved Problems

Problem 1 :

Find the vertex, focus, directrix, latus rectum of the following parabola :

x²  =  -16y

Solution :

x² = -16y is in the form of x² = -4ay. 

So, the given parabola opens down and symmetric about y-axis with vertex at (0, 0). 

Comparing x² = -16y and x² = -4ay, 

4a  =  16

Divide each side by 4. 

a  =  4

Focus : F(0, -a)  =  F(0, -4). 

Equation of latus rectum : y = -a ----> y = -4.

Equation of directrix : y = a ----> y = 4.

Problem 2 :

Find the vertex, focus, directrix, latus rectum of the following parabola :

y² - 8y - x + 19  =  0

Solution :

Write the equation of parabola in standard form. 

y² - 8y  =  x - 19

y² - 2(y)(4) + 4² - 4²  =  x - 19

(y - 4)² - 4²  =  x - 19

(y - 4)² - 16  =  x - 19

Add 16 to each side. 

(y - 4)²  =  (x - 3)

(y - 4)² = (x - 3) is in the form of (y - k)²  =  4a(x - h). 

So, the parabola opens up and symmetric about x-axis with vertex at (h, k) = (3, 4). 

Comparing (y - 4)² = (x - 3) and (y - k)²  =  4a(x - h), 

4a  =  1

Divide each side by 4.

a  =  1/4  =  0.25

Standard form equation of the given parabola : 

(y - 4)²  =  (x - 3)

Let Y = y - 4 and X = x - 3.

Then, 

Y²  =  X

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.