PARALLEL AND PERPENDICULAR LINES WORKSHEET

Problem 1 :

Think of each segment in the diagram as part of a line.

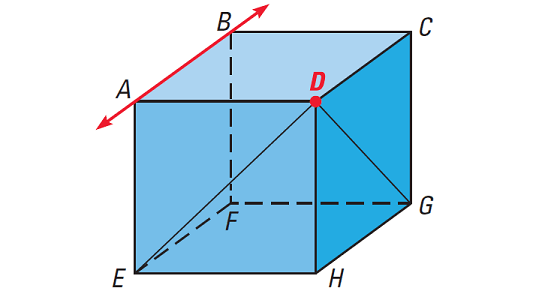
Which of the lines appear to fit the descriptions given below?

(i) Parallel to AB and contains D

(ii) Perpendicular to AB and contains D

(iii) Skew to AB and contains D

(iv) Name the plane(s) that contain D and appear to be parallel to plane ABE.

Problem 2 :

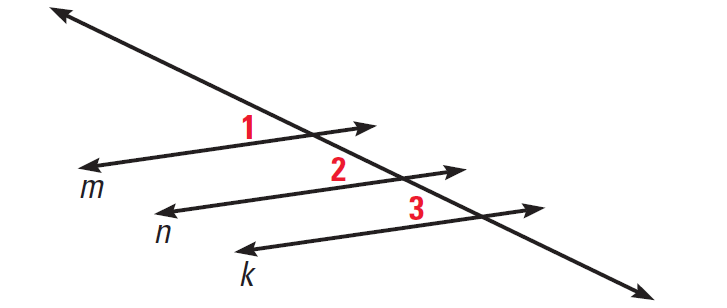
In the diagram given below, lines m, n and k represent three of the oars. If m||n and n||k, then prove m||k.

Problem 3 :

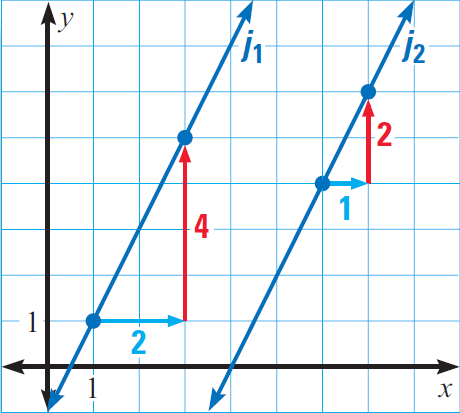
In the diagram given below, find the slope of each line. Determine whether the lines j₁ and j₂ are parallel.

Problem 4 :

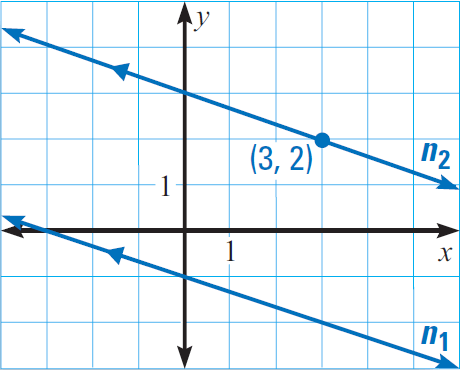
In the diagram given below, line n₁ has the equation

y = -ˣ⁄₃ -1

Line n₂ is parallel to the line n₁ and passes through the point (3, 2).

Write the equation of the line n₂.

Problem 5 :

Decide whether the lines are perpendicular.

Line 1 : y = ³ˣ⁄₄ + 2

Line 2 : y = -⁴ˣ⁄₃ - 3

Problem 6 :

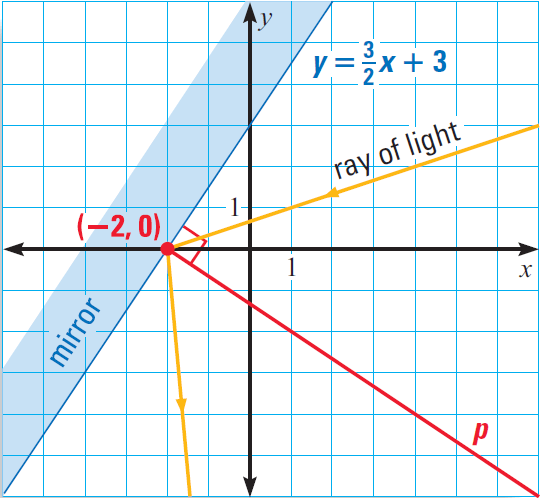
In the diagram given below, the equation y = ³ˣ⁄₂ + 3 represents a mirror. A ray of light hits the mirror at (-2, 0). What is the equation of the line p that is perpendicular to the mirror at this point?

Problem 7 :

Is it possible for two lines with negative slopes to be perpendicular?

Answers

1. Answer :

Which of the lines appear to fit the descriptions given below?

(i) Parallel to AB and contains D

(ii) Perpendicular to AB and contains D

(iii) Skew to AB and contains D

(iv) Name the plane(s) that contain D and appear to be parallel to plane ABE.

Solution (i) :

CD, GH and EF are all parallel to AB. But, only CD passes through D and is parallel to AB.

Solution (ii) :

BC, AD, AE and BF are all perpendicular to AB. But, only AD passes through D and is perpendicular to AB.

Solution (iii) :

DG, DH and DE all pass through D and are skew to AB.

Solution (iv) :

Only plane DCH contains D and is parallel to plane ABE.

2. Answer :

3. Answer :

Line j₁ has a slope of

m₂ = ⁴⁄₂ = 2

Line j₂ has a slope of

m₂ = ²⁄₁ = 2

Since the slope of the lines j₁ and j₂ are equal, the lines j₁ and j₂ are parallel.

4. Answer :

The slope of the line n₁ is -⅓. Because the lines n₁ and n₂ are parallel, they have the same slope. So, the slope of the line n₂ is also -1/3.

Slope-intercept form equation of a line :

y = mx + b ----(1) 

Because the line n₂ is passing through (3, 2), substitute (x, y) = (3, 2) and m = -1/3.

2 = (-⅓)(3) + b

2 = -1 + b

Add 1 to both sides.

3 = b

The equation of the required line is

(1) ----> y = (-⅓)x + 3

y = -ˣ⁄₃ + 3

5. Answer :

When we compare the given equations to slope intercept equation of a line y = mx + b, we get

slope of line 1 = ³⁄₄

slope of line 2 = -⁴⁄₃

Multiply the slopes :

The product is

= (³⁄₄)x (-⁴⁄₃) 

= - 1

Since the product of slopes of the lines is -1, the given lines are perpendicular.

6. Answer :

The slope of the mirror is ³⁄₂. So, the slope of the line p is -⅔.

Let y = mx + b be the equation of the line p.

Substitute (x, y) = (-2, 0) and m = -⅔ to find the value of b.

0 = (-⅔)(-2) + b

0 = ⁴⁄₃ + b

Subtract 4/3 from both sides.

-⁴⁄₃ = b

So, the equation of the line p is

y = -²ˣ⁄₃ - ⁴⁄₃

7. Answer :

We already know that if two lines are perpendicular, then the product of the slopes is equal to -1.

If the slopes of two lines are negative, then their product can never be equal to -1.

So, it is NOT possible for two lines with negative slopes to be perpendicular.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.