PARALLEL LINES AND TRANSVERSAL WORKSHEET

Problem 1 :

Identify the pairs of angles in the diagram. Then make a conjecture about their angle measures.

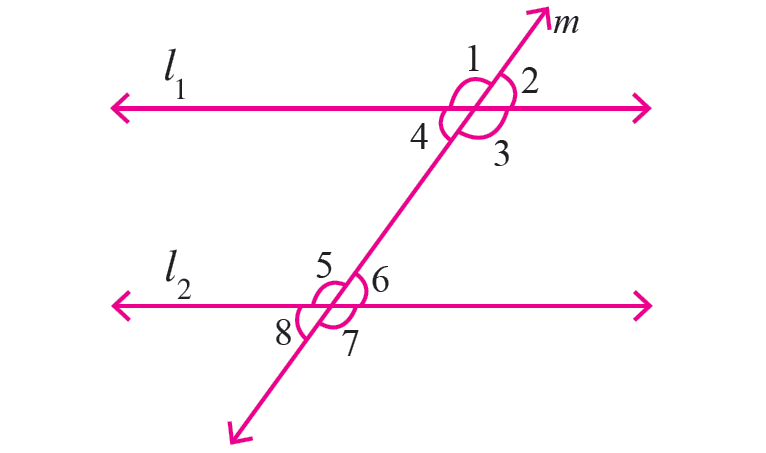
Problem 2 :

In the figure given below,  let the lines l₁ and l₂ be parallel and m is transversal. If ∠F = 65°, find the measure of each of the remaining angles.

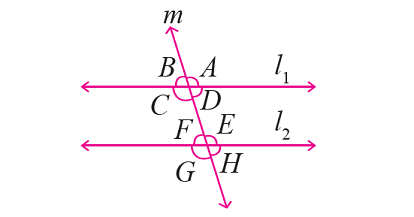
Problem 3 :

In the figure given below,  let the lines l₁ and l₂ be parallel and t is transversal. Find the value of 'x'.

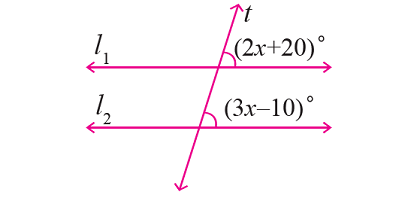
Problem 4 :

In the figure given below,  let the lines l₁ and l₂ be parallel and t is transversal. Find the value of 'x'.

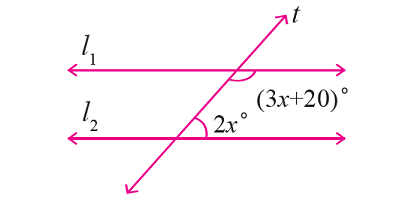
1. Answer :

2. Answer :

From the given figure,

∠F and ∠H are vertically opposite angles and they are equal.

Then, ∠H = ∠F ----> ∠H = 65°.

∠H and ∠D are corresponding angles and they are equal. 

Then, ∠D = ∠H ----> ∠D = 65.°

∠D and ∠B are vertically opposite angles and they are equal.

Then, ∠B = ∠D ----> ∠B = 65°.

∠F and ∠E are together form a straight angle.

Then, we have

∠F + ∠E = 180°

Substitute ∠F = 65°.

∠F + ∠E = 180°

65° + ∠E = 180°

∠E = 115°

∠E and ∠G are vertically opposite angles and they are equal.

Then, ∠G = ∠E ----> ∠G = 115°.

∠G and ∠C are corresponding angles and they are equal.

Then, ∠C = ∠G ----> ∠C = 115°.

∠C and ∠A are vertically opposite angles and they are equal.

Then, ∠A = ∠C ----> ∠A = 115°.

Therefore,

∠A = ∠C = ∠E = ∠G = 115°

∠B = ∠D = ∠F = ∠H = 65°

3. Answer :

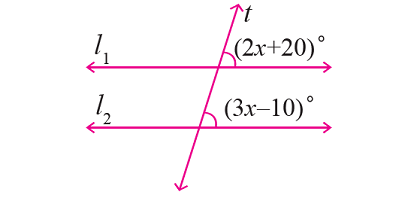
From the given figure,

∠(2x + 20)° and ∠(3x - 10)° are corresponding angles.

So, they are equal.

Then, we have

2x + 20 = 3x - 10

30 = x

4. Answer :

From the given figure,

∠(3x + 20)° and ∠2x° are consecutive interior angles.

So, they are supplementary.

Then, we have

3x + 20 + 2x = 180

5x + 20 = 180

5x = 160

x = 32

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.