PARALLEL LINES IN THE COORDINATE PLANE

Parallel lines are the lines that never intersect.

In the coordinate plane, they would look like as shown below.

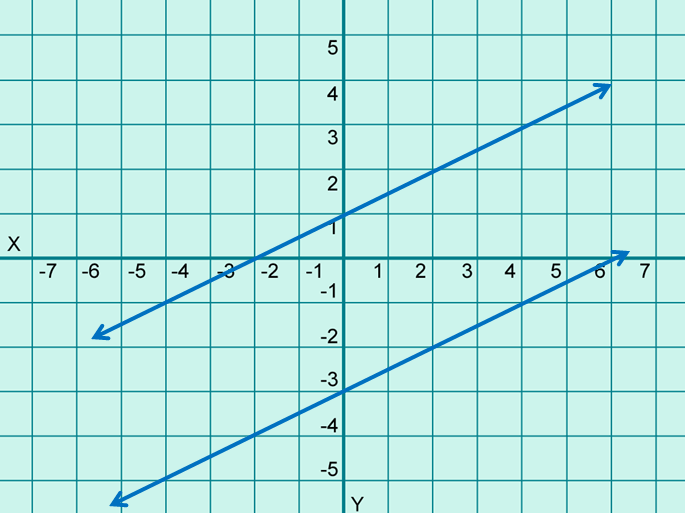
If we take a closer look at these two lines, the slope of both the lines is 1/2.

This can be generalized to any pair of parallel lines. Parallel lines always have the same slope and different y-intercepts.

Postulate (Slopes of Parallel Lines) :

In a coordinate plane, two lines are parallel if and only if they have the same slope.

Slope of a Line in Coordinate Plane

The slope of a non vertical line is the ratio of the vertical change (the rise) to the horizontal change (the run).

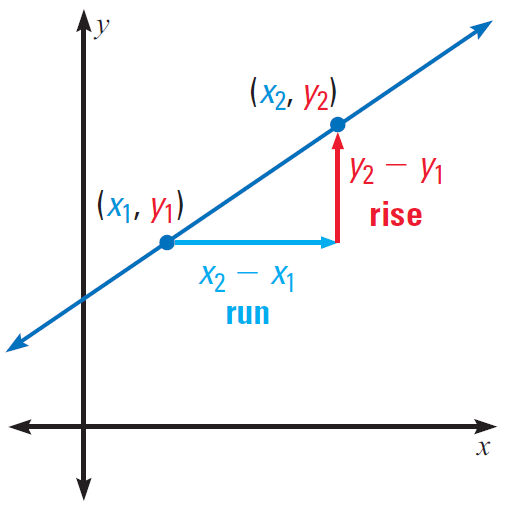
If the line passes through the points (x₁, y₁) and (x₂, y₂), then the slope is given by

Slope = rise/run

Slope = (y₂ - y₁)/(x₂ - x₁)

Usually, slope is represented by the variable m.

Example 1 :

In the diagram given below, find the slope of each line. Determine whether the lines j₁ and j₂ are parallel.

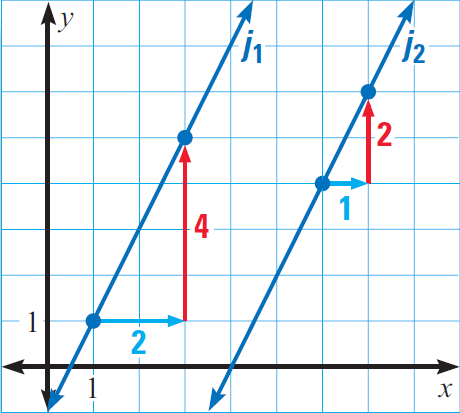
Solution :

Line j₁ has a slope of

m₂ = 4/2

= 2

Line j₂ has a slope of

m₂ = 2/1

= 2

Since the slope of the lines j₁ and j₂ are equal, the lines j₁ and j₂ are parallel.

Example 2 :

In the diagram given below, find the slope of each line. Which lines are parallel?

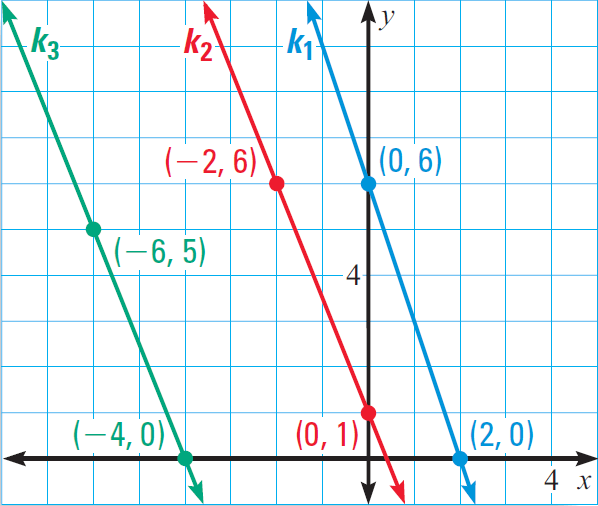
Solution :

Part 1 :

Find the slope of the line k₁. Line k₁ is passing through the points (0, 6) and (2, 0).

Let (x₁, y₁) = (0, 6) and (x₂, y₂) = (2, 0).

Slope (k₁) = (y₂ - y₁)/(x₂ - x₁)

= (0 - 6)/(2 - 0)

= -6/2

= - 3

Part 2 :

Find the slope of the line k₂. Line k₂ is passing through the points (-2, 6) and (0, 1).

Let (x₁, y₁) = (-2, 6) and (x₂, y₂) = (0, 1).

Slope (k₂) = (y₂ - y₁)/(x₂ - x₁)

= (1 - 6)/[0 -(-2)]

 = (1 - 6)/[0 + 2]

= -5/2

Part 3 :

Find the slope of the line k₃. Line k₃ is passing through the points (-6, 5) and (-4, 0).

Let (x₁, y₁) = (-6, 5) and (x₂, y₂) = (-4, 0).

Slope (k₃) = (y₂ - y₁)/(x₂ - x₁)

= (0 - 5)/[-4 - (-6)]

= -5/(-4 + 6)

= -5/2

Compare the slopes. Because k₂ and k₃ have the same slope, they are parallel. Line k₁ has a different slope, so it is not parallel to either of the lines.

Example 3 :

Write an equation of the line through the point (2, 3) that has a slope 5.

Solution :

Slope-intercept form equation of a line :

y = mx + b ----(1) 

Substitute (x, y) = (2, 3) and m = 5.

3 = 5(2) + b

Simplify.

3 = 10 + b

Subtract 3 from both sides.

-7 = b

The equation of the required line is

(1)----> y = 5x - 7

Example 4 :

In the diagram given below, line n₁ has the equation

y = -x/3 -1

Line n₂ is parallel to the line n₁ and passes through the point (3, 2).

Write the equation of the line n₂.

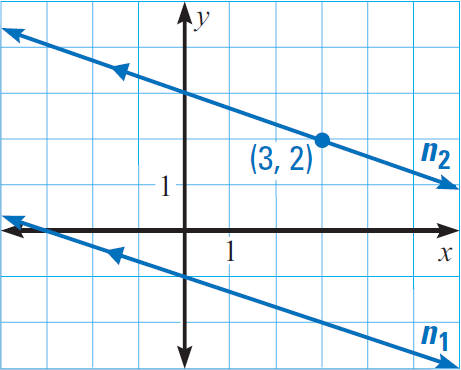
Solution :

The slope of the line n₁ is -1/3. Because the lines n₁ and n₂ are parallel, they have the same slope. So, the slope of the line n₂ is also -1/3.

Slope-intercept form equation of a line :

y = mx + b ----(1) 

Because the line n₂ is passing through (3, 2), substitute

(x, y) = (3, 2) and m = -1/3

2 = (-1/3)(3) + b

Simplify.

2 = -1 + b

Add 1 to both sides.

3 = b

The equation of the required line is

(1)----> y = (-1/3)x + 3

y = -x/3 + 3

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.