PARTIAL FRACTIONS EXAMPLES
Partial Fractions Examples :
Here we are going to see some example problems on partial fractions.
Partial Fractions Examples
Example 1 :
Resolve into partial fractions.
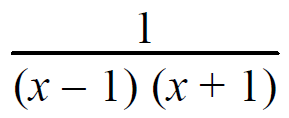
Solution :
1/(x - 1) (x + 1) = A/(x - 1) + B/(x + 1)
1/(x - 1) (x + 1) = A(x + 1) + B(x - 1)/(x - 1)(x + 1)
Since we have same denominators on both side, we can equate the numerators.
1 = A(x + 1) + B(x - 1) ------(1)
The constants A and B can also be found by successively giving suitable values for x.
To find A, put x = 1 in (1)
To find B, put x = -1 in (1)
|
1 = A(1 + 1) + B(1 - 1) 1 = 2A + B (0) 1 = 2A + 0 2A = 1 ===> A = 1/2 |
1 = A(-1 + 1) + B(-1 - 1) 1 = A(0) + B (-2) 1 = 0 - 2B -2B = 1 ===> B = -1/2 |
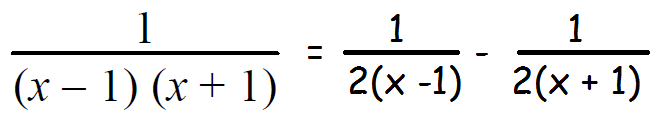
Example 2 :
Resolve into partial fractions.
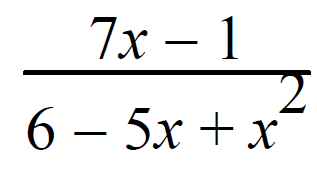
Solution :
7x - 1/(x2-5x + 6) = 7x - 1/(x - 3) (x - 2)
7x - 1/(x - 3) (x - 2) = A/(x - 3) + B/(x - 2)
7x - 1/(x - 3) (x - 2) = A(x - 2) + B(x - 3)/(x - 3)(x - 2)
Since we have same denominators on both side, we can equate the numerators.
7x - 1 = A(x - 2) + B(x - 3) ------(1)
The constants A and B can also be found by successively giving suitable values for x.
To find A, put x = 3 in (1)
To find B, put x = 2 in (1)
|
7(3) - 1 = A(3-2)+B(3-3) 21 - 1 = 1A + B (0) 20 = A + 0 A = 20 |
7(2) - 1 = A(2-2)+B(2-3) 14 - 1 = A(0) + B (-1) 13 = 0 - B B = -13 |
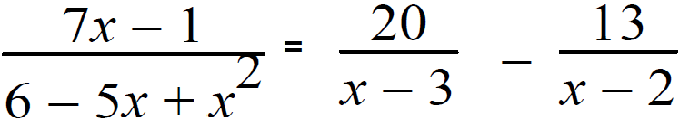
Example 3 :
Resolve into partial fractions.
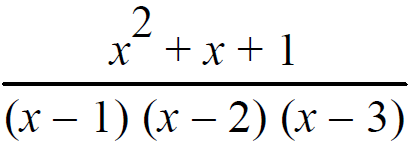
Solution :
(x2+ x + 1)/(x-1)(x-2)(x-3) = A/(x-1) + B/(x-2) + C/(x-3)
Taking L.C.M
= A(x-2)(x-3) + B(x-1)(x-3) + C(x-2)(x-1)/(x-1)(x-2)(x-3)
Since we have same denominators on both side, we can equate the numerators.
x2+ x + 1 = A(x-2)(x-3) + B(x-1)(x-3) + C(x-2)(x-1) ----(1)
The constants A, B and C can also be found by successively giving suitable values for x.
To find A, put x = 1 in (1)
To find B, put x = 2 in (1)
To find C, put x = 3 in (1)
|
If we put x = 1, both B and C will become zero. |
12+ 1 + 1 = A(1-2)(1-3) 3 = A(-1)(-2) 2A = 3 ==> A = 3/2 | |
|
If we put x = 2, both A and C will become zero. |
22+ 2 + 1 = B(2-1)(2-3) 4 + 2 +1 = B(1)(-1) 7= -B ==> B = -7 | |
|
If we put x = 3, both C and B will become zero. |
32+ 3 + 1 = C(3-2)(3-1) 9 + 3 + 1 = C(1)(2) 13 = 2C ==> C = 13/2 |
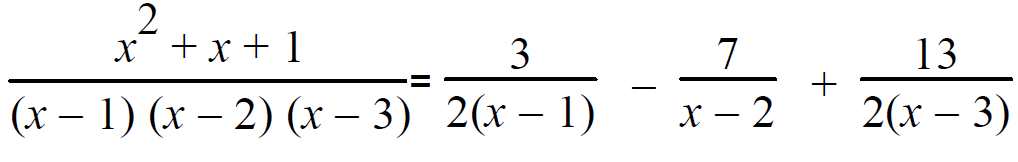
Example 4 :
Resolve into partial fractions.
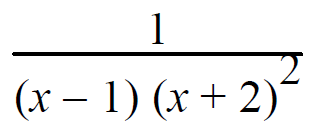
Solution :
1/(x-1)(x+2)2 = A/(x-1) + B/(x+2) + C/(x+2)2
Taking L.C.M
1/(x-1)(x+2)2 = A(x+2)2 + B(x-1)(x+2) + C(x-1)/(x-1)(x+2)2
Since we have same denominators on both side, we can equate the numerators.
1 = A(x+2)2 + B(x-1)(x+2) + C(x-1) ----(1)
By equating the coefficients of x2, x and constant terms respectively, we get
A + B = 0 -------(2)
4A + B + C = 0 -------(3)
4A - 2B - C = 1 -------(4)
By adding the equations (3) and (4) we get,
00000000000004A + B + C = 000000000000000000000
00000000000004A - 2B - C = 10000000000000000000
000000000000-------------------0000000000000000000
0000000000008A - B = 1------(5)00000000000000000
(5) + (2)
A + B + 8A - B = 0 + 1
9A = 1 ==> A = 1/9
|
Substituting the value of A in (2), we get 1/9 + B = 0 B = -1/9 |
Substituting the values of A and B in (3), we get 4(1/9) + (-1/9) + C = 0 4/9 - 1/9 + C = 0 (4 - 1 + 9C)/9 = 0 3 + 9C = 0 9C = -3 C = -3/9 ==> -1/3 |
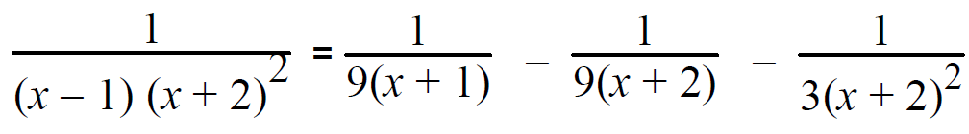
Example 5 :
Resolve into partial fractions.
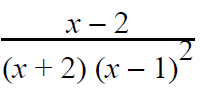
Solution :
(x - 2)/(x+2)(x-1)2 = A/(x + 2) + B/(x - 1) + C/(x - 1)2
Taking L.C.M
(x-2)/(x+2)(x-1)2 = A(x-1)2+B(x-1)(x+2)+C(x+2)/(x+2)(x-1)2
Since we have same denominators on both side, we can equate the numerators.
x - 2 = A(x - 1)2 + B(x - 1)(x + 2) + C(x + 2) --(1)
By equating the coefficients of x2, x and constant terms respectively, we get
A + B = 0 -------(2)
-2A + B + C = 1 -------(3)
A - 2B + 2C = -2 -------(4)
2 x (3) - (4)
2(-2A + B + C) - (A - 2B + 2C) = 2 - (-2)
-4A - A + 2B + 2B + 2C - 2C = 2 + 2
-5A + 4B = 4 -------(5)
5 x (2) + (5)
5A + 5B + (-5A + 4B) = 0 + 4
5A + 5B -5A + 4B = 4
9B = 4 ==> B = 4/9
|
Substituting the value of B in (2), we get A + 4/9 = 0 A = -4/9 |
Substituting the values of A and B in (3), we get -2(-4/9) + 4/9 + C = 1 8/9 + 4/9 + C = 1 (8 + 4 + 9C)/9 = 1 12 + 9C = 9 9C = -3 C = -1/3 |
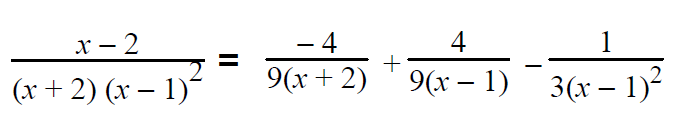
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 106)
Feb 04, 25 08:16 AM
Digital SAT Math Problems and Solutions (Part - 106) -
SAT Math Resources (Videos, Concepts, Worksheets and More)
Feb 04, 25 08:15 AM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Digital SAT Math Problems and Solutions (Part - 107)
Feb 04, 25 08:11 AM
Digital SAT Math Problems and Solutions (Part - 107)