PASCAL TRIANGLE AND BINOMIAL EXPANSION WORKSHEET

Expand the following binomials using pascal triangle :

Problem 1 :

(3x + 4y)⁴

Problem 2 :

(x - 4y)⁴

Answers

1. Answer :

(3x + 4y)⁴

Pascal's Triangle :

In (3x + 4y)⁴, the exponent is '4'.

So, let us take the row in the above pascal triangle which is corresponding to 4th power.

That is,

1    4    6    4    1

Step 1 :

In the first term, we have to take only '3x' with power '4' [This is the exponent of (3x + 4y)].

Then, the first term is

= (3x)⁴

= 81x⁴

Step 2 :

In the second term, we have to take both '3x' and '4y'.

For '3x', we have to take exponent '1' less than the exponent of '3x' in the previous term.

For '4y', we have to take exponent '1'.

Then, the second term is

= (3x)³(4y)

= (27x³)(4y)

= 108x³y

Step 3 :

In the third term also, we have to take both '3x' and '4y'.

For '3x', we have to take exponent '1' less than the exponent of '3x' in the previous term.

For '4y', we have to take exponent '2'.

Then, the second term is

= (3x)²(4y)²

= (9x²)(16y²)

= 144x²y²  

(We have to continue this process, until we get the exponent '0' for 'a')

Step 4 : 

When we continue the process said in step 3, the term in which we get exponent '0' for '3x' will be the last term.

In the last term, we will have only '4y' with power '4' [This is the exponent of (3x + 4y)]

Then, the last term is

= (4y)⁴

= 256y⁴

The four steps explained above have been summarized in the diagram shown below.

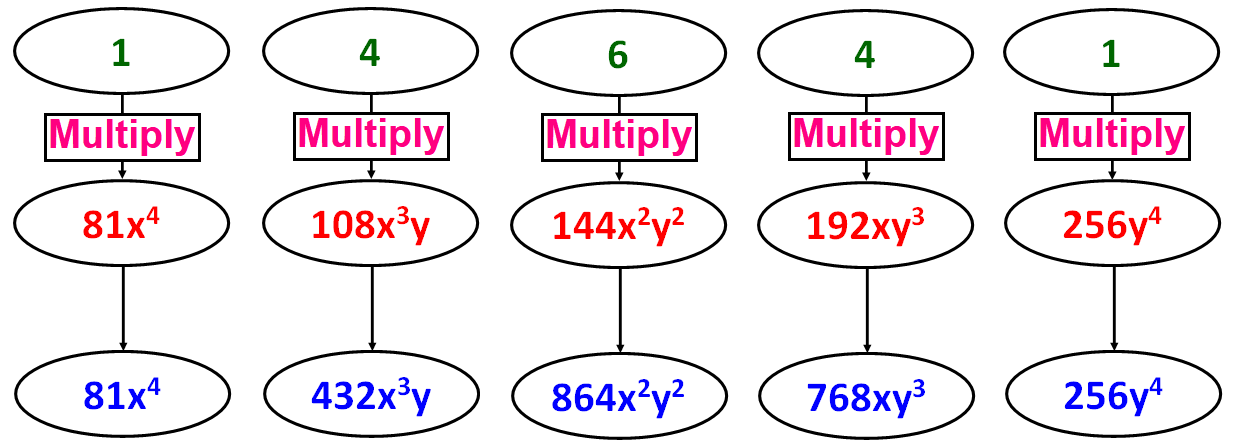
Hence, the expansion of (3x + 4y)⁴ is

(3x + 4y)⁴  =  81x⁴ + 432x³y + 864x²y² + 768xy³ + 256y⁴

2. Answer :

(x - 4y)⁴

We can follow the steps explained in problem 1 and get the expansion of (x - 4y)⁴.

But we have negative sign in (x - 4y)⁴.

So, we have to take positive and negative signs alternatively staring with positive sign for the first term. 

Hence, the expansion of (x - 4y)⁴ is

(x - 4y)⁴ = x⁴ - 4(x³)(4y) + 6(x²)(4y)² - 4(x)(4y)³ + (4y)⁴

(x - 4y)⁴ = x⁴ - 16x³y + 6(x²)(16y²) - 4(x)(64y³) + 256y⁴

(x - 4y)⁴ = x⁴ - 16x³y + 96x²y² - 256xy³ + 256y⁴

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.