PATH WAYS

Example 1 :

A plot is 100 m long and 60 m broad. A path 5 m wide runs breadth wise across the ground in the middle. Find the area of the path.

Solution :

In the bellow figure the shaded portion is the path way. To find the area of pathway we can take the length as 60 m and breadth as 5 m.

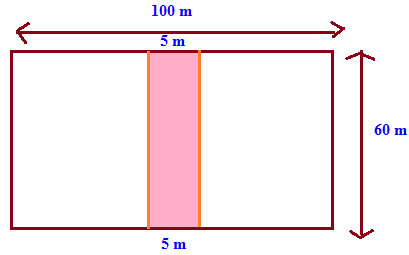
Area of pathway  =  L x B

=  60 x 5

= 300 m²

Example 2 :

Find the area of the shaded portion in the below figure.

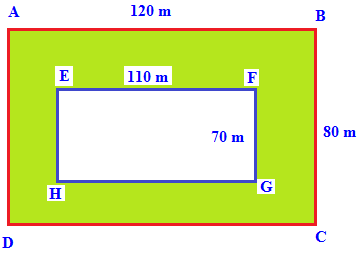
Solution :

Area of shaded portion

=  Area of rectangle ABCD - Area of rectangle EFGH

Area of rectangle ABCD :

Length (AB)  =  120 m

Breadth (BC)  =  80 m

Area of rectangle ABCD  =  Length x width

=  120 x 80

=  9600 m²

Area of rectangle EFGH :

Length (EF)  =  110 m

Breadth (FG)  = 70 m

Area of rectangle EFGH  =  Length x width

=  110 x 70

=  7700 m²

Area of shaded portion

=  Area of rectangle ABCD - Area of rectangle EFGH

=  9600 - 7700

=  1900 m²

Example 3 :

There is a hall 40 m in length and 30 m in breadth. There is verandah 5 m wide surrounding the hall on all the four sides out side. Find the area of the verandah.

Solution :

First let us draw the diagram based on the given details.

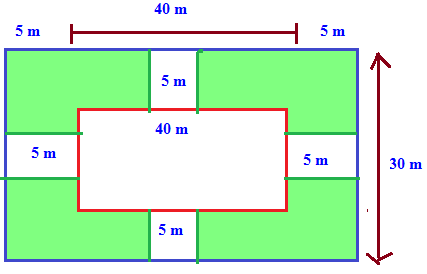
The hall is a rectangle. The hall and verandahs which is out side is bigger rectangle.

Then length of bigger rectangle = 40 + 5 + 5

=  50 m

Breadth of bigger rectangle = 30 + 5 + 5

= 40 m

Area of hall and verandahs  =  50 x 40

=  2000 m²

Area of the hall  =  40 x 30

=  1200 m²

Area of verandahs  =  2000 - 1200

=  800 m²

Example 4 :

Find the area of a ring whose outer radius is 20 cm and inner radius is 15 cm respectively.

Solution :

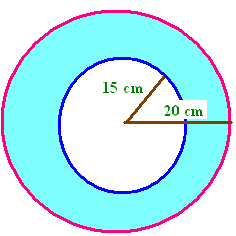
Let R and r be the radius of the outer, inner circle.

Area of outer circle  =  ΠR²

Area of inner circle  =  Πr²

Radius of outer circle (R)  =  20 cm

Radius of the inner circle (r)  =  15 cm

Area of ring (shaded portion)   

=  Area of outer circle - area of inner circle

=  ΠR² -  Πr²

=  Π (R² - r²)

=  Π (20² - 15²)

=  Π x (400 - 225)

=  Π x 175

=  (22/7) x 175

=  22 x 25 

=  550 cm²

Example 5 :

A circular garden, of circumference 88 m is surrounded by a pathway of width 3.5 m. Ajay wants to put fence around the pathway. What is the cost of fencing the pathway at the rate of $70 per meter?

Solution :

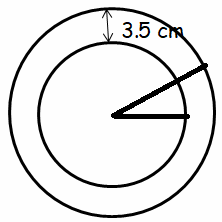
Circumference of the circle = 88 m

2Πr = 88

r = 88/2Π

r = 14.01

Approximately 14 m.

Radius of large circle = 14 + 3.5

= 17.5 m

Circumference of large circle = 2ΠR

= 2 x 3.14 x 17.5

= 109.9 m²

Cost of fencing the pathway = $70 per square meter

Total cost = 109.9 (70)

= $7693

Example 6 :

Two concentric circles of radius 8 cm and 5 cm are shown below, and a sector forms an angle of 60° at the center O. What is the area of the shaded region?

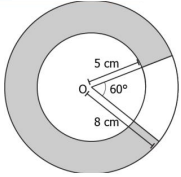
Solution :

Area of pathway = Area of large circle - area of small circle

= Π (R² - r²)

= Π (8² - 5²)

= 3.14 (64 - 25)

= 122.46 cm²

Area of path ways in the outer circle

= Area of large sector - area of small sector

= (θ/360)Π (R² - r²)

= (60/360)Π (8² - 5²)

= (1/6) x 3.14(64 - 25)

= (1/6) x 3.14 x 39

= 20.41 cm²

Area of shaded region = 122.46 - 20.41

= 102.05 cm²

Example 7 :

The above right sided figure depicts a racing track whose left and right ends are semi-circular. The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find the area of the track.

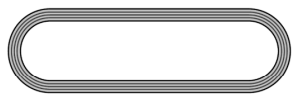
Solution :

Area of the rectangular shape = (106 x 80) - (106 x 60)

= 106(80 - 60)

= 106 x 20

= 2120 m²

Area of semicircular portions = 2Π(R² - r²)/2

= Π(R² - r²)

= 3.14(40² - 30²)

= 3.14(1600 - 900)

= 3.14(700)

= 2198 m²

Total area = 2120 + 2198

= 4318 m²

Example 8 :

A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope.

Find

a) the area of that part of the field in which the horse can graze.

b) The increase in the grazing area if the rope were 10 m long instead of 5 m. (Use π = 3.14)

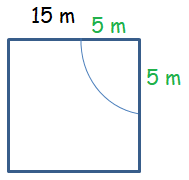
Solution :

a) Area of the field the horse can graze = (1/4)Πr²

= (1/4) x 3.14 x 5²

= 19.625 m²

a) Area of the field the horse can graze after increasing the rope length

= (1/4)Πr²

= (1/4) x 3.14 x 10²

= 78.5 m²

Related pages

• Area of sector
• Perimeter of sector
• Length of arc
• Finding the area of a circle
  
• Finding circumference of a circle
  
• Area and perimeter of semicircle
  
• Area and perimeter of quadrant
  
• Area and perimeter of a square
• Perimeter and area of rectangle
  
• Area and perimeter of a triangle worksheet
  
• Area of parallelogram
• Area of rhombus
• Area around circle
• Area of combined shapes

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.