PERIMETER AND AREA OF RECTANGLE
In this section, you will learn how to find perimeter and area of a rectangle.
A rectangle is a four-sided closed figure where the lengths of opposite sides will be equal and each vertex angle will be right angle or 90o as shown below.
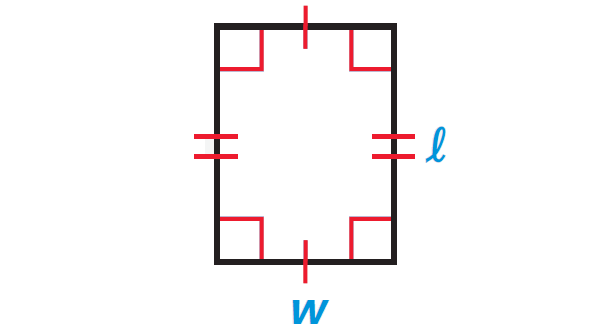
Formula for Perimeter of Rectangle
Let l be the length and w be the width of a rectangle.
Then, the formula for perimeter of the rectangle :
Perimeter = 2(l + w)
Formula for Area of a Rectangle
To get the area of any rectangle, we have to multiply its length and width.
Let l be the length and w be the width of a rectangle.
Then, the formula for area of the rectangle :
Area = l ⋅ w
Example 1 :
Find the perimeter of the figure shown below.
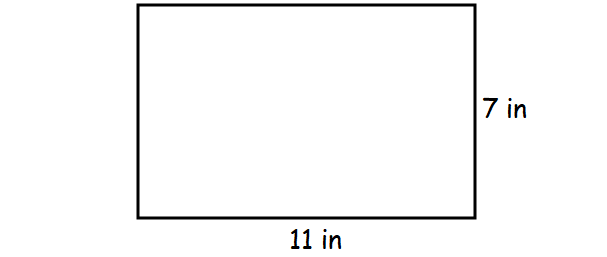
Solution :
The figure shown above is a rectangle with 7 inches length and 11 inches width.
Formula for perimeter of a rectangle :
= 2(l + w)
Substitute 7 for l and 11 for w.
= 2(7 + 11)
= 2(18)
= 36
So, the perimeter of the rectangle is 36 inches.
Example 2 :
The perimeter of a rectangle is 42 cm. If its width is 3 more than twice its length, then find its length and with.
Solution :
Let x be the length of the rectangle.
Then, the width is (2x + 3)
Perimeter of the rectangle = 42 cm
2(l + w) = 42
Divide each side by 2.
l + w = 21
Substitute x for l and (2x + 3) for w.
x + (2x + 3) = 21
x + 2x + 3 = 21
3x + 3 = 21
Subtract 3 from each side.
3x = 18
Divide each side by 3.
x = 6
Therefore, the length is 6 cm.
And the width is
2x + 3 = 2(6) + 3
2x + 3 = 12 + 3
2x + 3 = 15
So, the length and width of the rectangle are 6 cm and 15 cm respectively.
Example 3 :
Find the area of the figure shown below.
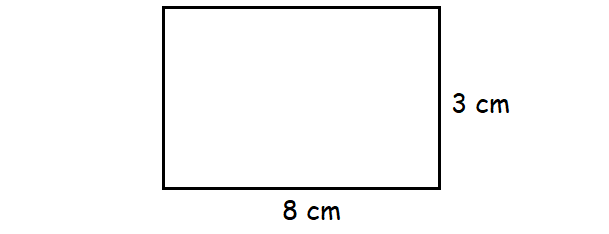
Solution :
The figure shown above is a rectangle with 3 cm length and 8 cm width.
Formula for area of a rectangle :
= l ⋅ w
Substitute 3 for l and 8 for w.
= 3 ⋅ 8
= 24
So, the area of the rectangle is 24 square cm.
Example 4 :
Find the area of the figure shown below.
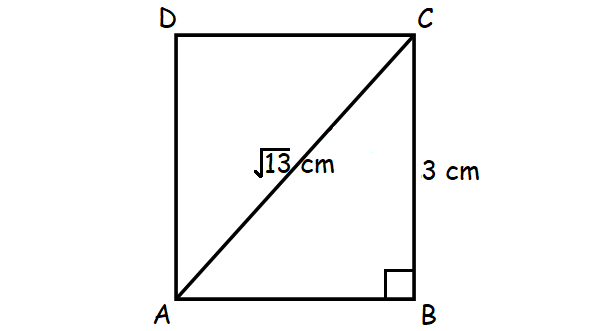
Solution :
The figure shown above is a rectangle with 3 cm length and the measure of one the diagonals is √13 cm.
To find the area of a rectangle, we have to know its length and width. In the figure shown above, length is given, that is 3 cm. So, find its width.
In the figure shown above, consider the right triangle ABC.
By Pythagorean Theorem, we have
AB2 + BC2 = AC2
Substitute.
AB2 + 32 = (√13)2
Simplify and solve for AB.
AB2 + 9 = 13
Subtract 9 from each side.
AB2 = 4
Find positive square root on both sides.
√AB2 = √4
AB = 2
Therefore, the width of the rectangle is 2 cm.
Formula for area of a rectangle :
= l ⋅ w
Substitute 3 for l and 2 for w.
= 3 ⋅ 2
= 6
So, the perimeter of the rectangle is 6 square cm.
Example 5 :
The length and width of a rectangular shaped wall are 8 ft and 12 ft respectively. If the cost of painting is $8.50 per square feet, then find the total cost of painting for the wall.
Solution :
To find the total cost of painting for the wall, we have to know its area. Because the wall is rectangle shaped, we can use the formula for area of a rectangle to find the area of the wall.
Formula for area of a rectangle :
= l ⋅ w
Substitute 8 for l and 12 for w.
= 8 ⋅ 12
= 96
So, the area of the wall is 96 square ft.
The cost of painting is $8.50 per square ft.
Then, the total cost of painting for 96 square ft :
= 96 ⋅ 8.50
= 816
So, the total cost of painting the wall is $816.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 146)
Apr 18, 25 06:52 AM
Digital SAT Math Problems and Solutions (Part - 146) -
Logarithmic Derivative Problems and Solutions
Apr 16, 25 09:25 PM
Logarithmic Derivative Problems and Solutions -
Digital SAT Math Problems and Solutions (Part - 145)
Apr 16, 25 12:35 PM
Digital SAT Math Problems and Solutions (Part - 145)

