PERIMETER OF A TRIANGLE WORKSHEET

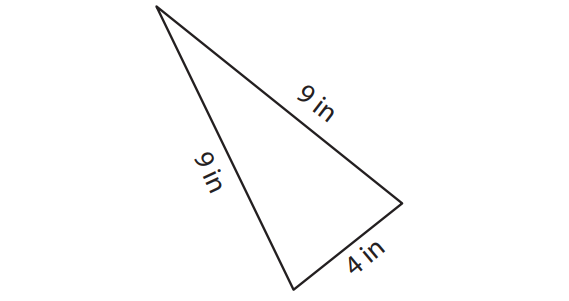
1.  Find the perimeter of the triangle shown below. 

2.  The sides of a triangle are 12 cm, 6 cm and 8 cm. Find the perimeter of the triangle.

3.  The length of each of side of an equilateral triangle is 7 in. Find the perimeter of the triangle.   

4.  The length of each of the equal sides of an isosceles triangle is 3 cm and the length of the third side is 5 cm. Find the perimeter of the triangle.  

5.  The sides of a triangle are 2x, 3x and 4x. If the perimeter of the triangle is 81 in, then find the length of each side of the triangle. 

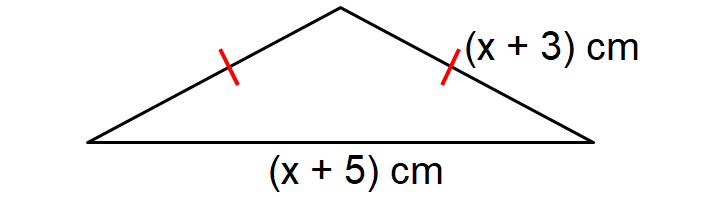
6.  If the perimeter of the triangle shown below is 101 cm, find the value of x. 

7.  In a triangle, the length of the first side is 1 more than the length of the second side and the length of the second side is 1.5 times the length of the third side. If the length of the third side is 10 cm, find the perimeter of the triangle. 

8.  In a triangle, the length of the first side of is 3 units more than the second side and the length of the second side is 5 units more than the third side. If the perimeter of the triangle is 85 units, find the length of the sides of the triangles.

9.  The length of each of the equal sides of an isosceles triangle is 4 cm longer than the base. If the perimeter of the triangle is 62 cm, find the length of the sides of the triangles.

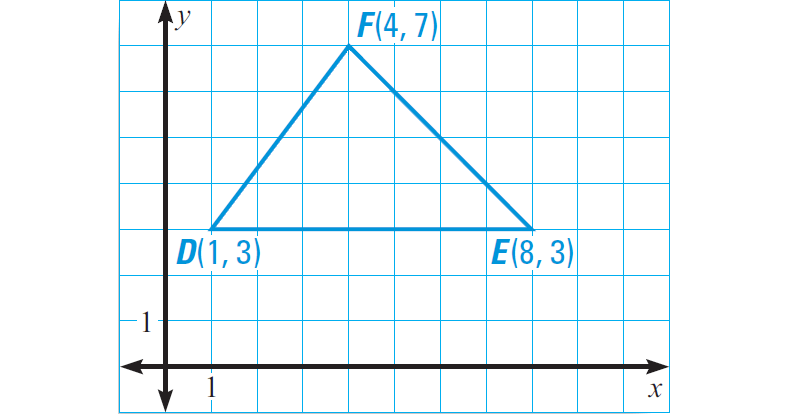
10.  Find the perimeter of the triangle defined by the following points : 

D(1, 3), E(8, 3) and F(4, 7)

1. Answer :

Perimeter of the triangle :

=  9 + 9 + 4

=  22 in

2. Answer  : 

Perimeter of the triangle : 

=  12 + 6 + 8

=  26 cm

3. Answer :

Perimeter of the triangle :

=  7 + 7 + 7

=  21 in

4. Answer :

Perimeter of the triangle :

=  3 + 3 + 5

=  11 cm

5. Answer :

Perimeter of the triangle  =  81 in

2x + 3x + 4x  =  81

9x  =  81

Divide each side by 9.

x  =  9

2x  =  2(9)  =  18

3x  =  3(9)  =  27

4x  =  4(9)  =  36

The lengths of the sides of the triangle are 18in, 27 in and 36 in. 

6. Answer :

The above triangle is an isosceles triangle and the length of each of the two equal sides is (x + 3) cm. 

Perimeter of the triangle  =  101 cm

(x + 3) + (x + 3) + (x + 5)  =  101

x + 3 + x + 3 + x + 5  =  101

3x + 8  =  101

Subtract 8 from each side. 

3x  =  93

Divide each side by 3. 

x  =  31

7. Answer : 

Given : Length of third side is 10 cm.

Then, 

the length of the second side  =  1.5(10)  =  15 cm

the length of the first side  =  15 + 1  =  16 cm

Perimeter of the triangle :

=  16 + 15 + 10

=  41 cm

8. Answer : 

Let x be the length of the third side of the triangle. 

Then, 

the length of the second side  =  x + 5

the length of the first side  =  x + 5 + 3  =  x + 8

Perimeter of the triangle  =  85 units

(x + 8) + (x + 5) + x  =  85

x + 8 + x + 5 + x  =  85

3x + 13  =  85

Subtract 13 from each side.

3x  =  72

Divide each side by 3.

x  =  24

Length of the 3^rd side : 24

Length of the 2^nd side : 24 + 5  =  29

Length of the 1^st side : 29 + 3  =  32

The lengths of the sides of the triangle are 24 units, 29 units and 32 units. 

9. Answer : 

Let x be the length of each of the two equal sides and y be the length of the base.

Then, x = y + 4. 

Perimeter of the triangle  =  62 cm

x + x + y  =  62

2x + y  =  62

Substitute x = y + 4. 

2(y + 4) + y  =  62

2y + 8 + y  =  62

3y + 8  =  62

Subtract 8 from each side. 

3y  =  54

Divide each side by 3. 

y  =  18

x  =  18 + 4

=  22

The length of the sides of the triangle are 22 cm, 22 cm and 18 cm.  

10. Answer : 

Plot the points in the coordinate plane. Draw the height from F to the side DE. Label the point where the height meets DE as G. Point G has coordinates (4, 3). 

Length of DE : 

=  8 - 1

=  7

Use distance formula to find the length of EF and FD.

Distance Formula :

=  √[(x₂ - x₁)² + (y₂ - y₁)²]

Length of EF : 

(x₁, y₁)  =  E(8, 3)

(x₂, y₂)  =  F(4, 7)

EF  =  √[(4 - 8)² + (7 - 3)²]

EF  =  √[(-4)² + (4)²]

EF  =  √[16 + 16]

EF  =  √32

EF  =  √(4 ⋅ 4 ⋅ 2)

EF  =  4√2

Length of FD : 

(x₁, y₁)  =  F(4, 7)

(x₂, y₂)  =  D(1, 3)

FD  =  √[(1 - 4)² + (3 - 7)²]

FD  =  √[(-3)² + (-4)²]

FD  =  √[9 + 16]

FD  =  √25

FD  =  5

Perimeter of the triangle :

=  5 + 7 + 4√2

=  (12 + 4√2) units

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.