PERIMETER OF SECTOR WORKSHEET

Problem 1 :

Find the perimeter of the sector PQR shown below. 

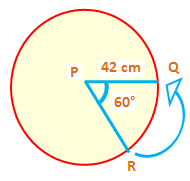
Problem 2 :

Find the perimeter of the sector AOB shown below. 

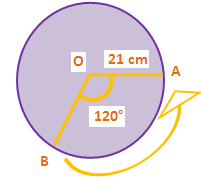
Problem 3 :

Find the perimeter of the sector BAP shown below. 

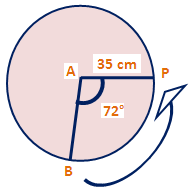
Problem 4 :

Find the perimeter of the sector PQR shown below. 

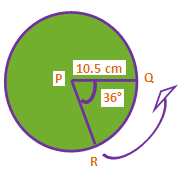
Problem 5 :

Find the perimeter of sector whose area is 324 square cm and the radius is 27 cm.

Problem 6 :

Find the length of arc, if the perimeter of sector is 45 cm and radius is 10 cm.

Problem 7 :

Find the radius of sector whose perimeter of the sector is 30 and length of the arc is 16 cm. 

Problem 8 :

Find the diameter of the circle which has a sector whose perimeter is 84 cm and length of arc of the sector is 56 cm. 

Solutions

Problem 1 :

Find the perimeter of the sector PQR shown below. 

Solution : 

Length of the arc is 

l  =  θ/360° ⋅ 2∏r

Substitute  θ  =  60°, r  =  42 and ∏  =  22/7.

l  =  60°/360° ⋅ 2 ⋅ 22/7 ⋅ 42

l  =  1/6 ⋅ 2 ⋅ 22 ⋅ 6

l  =  1 ⋅ 2 ⋅ 22

l  =  44 cm

Perimeter of sector is 

=  l + 2r

Substitute l  =  44 and r  =  42. 

=  44 + 2(42)

=  44 + 84

=  128 cm

So, length of the arc is 128 cm. 

Problem 2 :

Find the perimeter of the sector AOB shown below. 

Solution : 

Length of the arc is 

l  =  θ/360° ⋅ 2∏r

Substitute  θ  =  120°, r  =  21 and ∏  =  22/7.

l  =  120°/360° ⋅ 2 ⋅ 22/7 ⋅ 21

l  =  1/3 ⋅ 2 ⋅ 22 ⋅ 3

l  =  1 ⋅ 2 ⋅ 22

l  =  44 cm

Perimeter of sector is 

=  l + 2r

Substitute l  =  44 and r  =  21. 

=  44 + 2(21)

=  44 + 42

=  86 cm

So, length of the arc is 86 cm. 

Problem 3 :

Find the perimeter of the sector BAP shown below. 

Solution : 

Length of the arc is 

l  =  θ/360° ⋅ 2∏r

Substitute  θ  =  72°, r  =  35 and ∏  =  22/7.

l  =  72°/360° ⋅ 2 ⋅ 22/7 ⋅ 35

l  =  1/5 ⋅ 2 ⋅ 22 ⋅ 5

l  =  1 ⋅ 2 ⋅ 22

l  =  44 cm

Perimeter of sector is 

=  l + 2r

Substitute l  =  44 and r  =  35. 

=  44 + 2(35)

=  44 + 70

=  114 cm

So, length of the arc is 114 cm. 

Problem 4 :

Find the perimeter of the sector PQR shown below. 

Solution : 

Length of the arc is 

l  =  θ/360° ⋅ 2∏r

Substitute  θ  =  36°, r  =  10.5 and ∏  =  22/7.

l  =  36°/360° ⋅ 2 ⋅ 22/7 ⋅ 10.5

l  =  1/10 ⋅ 2 ⋅ 22 ⋅ 1.5

l  =  66/10

l  =  6.6 cm

Perimeter of sector is 

=  l + 2r

Substitute l  =  6.6 and r  =  10.5. 

=  6.6 + 2(10.5)

=  6.6 + 21

=  27.6 cm

So, length of the arc is 27.6 cm. 

Problem 5 :

Find the perimeter of sector whose area is 324 square cm and the radius is 27 cm.

Solution :

Area of sector  =  324 cm²

rl / 2  =  324

Multiply each side by 2.

rl  =  648

Substitute 27 for r.

27l  =  648

Divide each side by 27.

l  =  24 cm

Perimeter of sector is

=  l + 2r

=  24 + 2(27)

=  24 + 54

=  78 cm

Problem 6 :

Find the length of arc, if the perimeter of sector is 45 cm and radius is 10 cm.

Solution :

Perimeter of sector  =  45 cm

l + 2r  =  45

Substitute 10 for r. 

l + 2 (10)  =  45

l + 20  =  45

l  =  45 - 10

l  =  35 cm

Problem 7 :

Find the radius of sector whose perimeter of the sector is 30 cm and length of the arc is 16 cm. 

Solution :

Perimeter of sector  =  30 cm

l + 2r  =  30

Substitute 16 for l. 

16 + 2r  =  30

Subtract 16 from each side. 

2r  =  14

Divide each side by 2.

r  =  7 cm

Problem 8 :

Find the diameter of the circle which has a sector whose perimeter is 84 cm and length of arc of the sector is 56 cm. 

Solution :

Perimeter of sector  =  84 cm

l + 2r  =  84

Substitute 56 for l. 

56 + 2r  =  84

Subtract 56 from each side. 

2r  =  28

Diameter  =  2 x Radius

Diameter  =  2r

Diameter  =  28 cm.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.