PERIMETER OF THE SECTOR

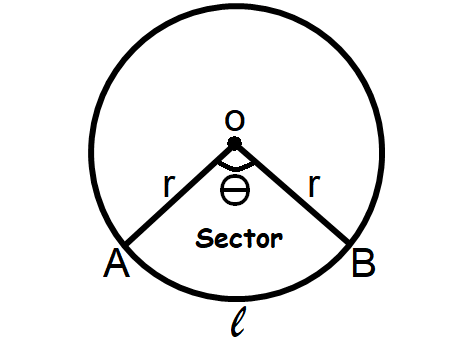
Formula to find perimeter of the sector is

=  l + 2r

where 'l' is the length of the minor arc AB. 

Formula to find length of the arc is 

l  =  θ/360° ⋅ 2∏r

Formula to find area of sector is 

A  =  θ/360° ⋅ ∏r² square units

or 

A  =  rl / 2 square units

Examples

Example 1 :

Find the perimeter of the sector PQR shown below. 

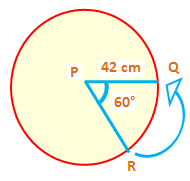
Solution : 

Length of the arc is 

l  =  θ/360° ⋅ 2∏r

Substitute  θ  =  60°, r  =  42 and ∏  =  22/7.

l  =  60°/360° ⋅ 2 ⋅ 22/7 ⋅ 42

l  =  1/6 ⋅ 2 ⋅ 22 ⋅ 6

l  =  1 ⋅ 2 ⋅ 22

l  =  44 cm

Perimeter of sector is 

=  l + 2r

Substitute l  =  44 and r  =  42. 

=  44 + 2(42)

=  44 + 84

=  128 cm

So, length of the arc is 128 cm. 

Example 2 :

Find the perimeter of the sector AOB shown below. 

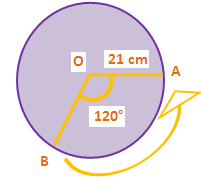
Solution : 

Length of the arc is 

l  =  θ/360° ⋅ 2∏r

Substitute  θ  =  120°, r  =  21 and ∏  =  22/7.

l  =  120°/360° ⋅ 2 ⋅ 22/7 ⋅ 21

l  =  1/3 ⋅ 2 ⋅ 22 ⋅ 3

l  =  1 ⋅ 2 ⋅ 22

l  =  44 cm

Perimeter of sector is 

=  l + 2r

Substitute l  =  44 and r  =  21. 

=  44 + 2(21)

=  44 + 42

=  86 cm

So, length of the arc is 86 cm. 

Example 3 :

Find the perimeter of sector whose area is 324 square cm and the radius is 27 cm.

Solution :

Area of sector  =  324 cm²

rl / 2  =  324

Multiply each side by 2.

rl  =  648

Substitute 27 for r.

27l  =  648

Divide each side by 27.

l  =  24 cm

Perimeter of sector is

=  l + 2r

=  24 + 2(27)

=  24 + 54

=  78 cm

Example 4 :

Find the length of arc, if the perimeter of sector is 45 cm and radius is 10 cm.

Solution :

Perimeter of sector  =  45 cm

l + 2r  =  45

Substitute 10 for r. 

l + 2 (10)  =  45

l + 20  =  45

l  =  45 - 10

l  =  35 cm

Example 5 :

Find the radius of sector whose perimeter of the sector is 30 cm and length of the arc is 16 cm. 

Solution :

Perimeter of sector  =  30 cm

l + 2r  =  30

Substitute 16 for l. 

16 + 2r  =  30

Subtract 16 from each side. 

2r  =  14

Divide each side by 2.

r  =  7 cm

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.