PERPENDICULARS AND BISECTORS WORKSHEET

Question 1 :

In the diagram shown below, MN is the perpendicular bisector of ST. 

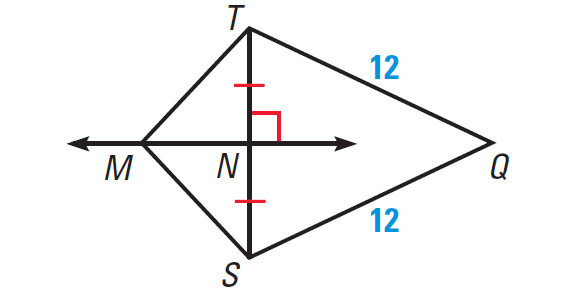
(a) What segment lengths in the diagram are equal ?

(b) Explain why Q is on MN ? 

Question 2 :

In the diagram shown below, D is on the bisector of ∠BAC, DB ⊥ AB, DC ⊥ AC. Prove that DB = DC. 

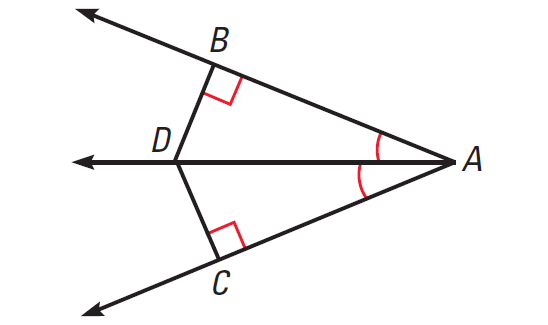
Question 3 :

Some roofs are built with wooden trusses that are assembled in a factory and shipped to the building site. In the diagram of the roof truss shown below, we are given that AB bisects ∠CAD and that ∠ACB and ∠ADB are right angles. What can be said about BC and BD ? 

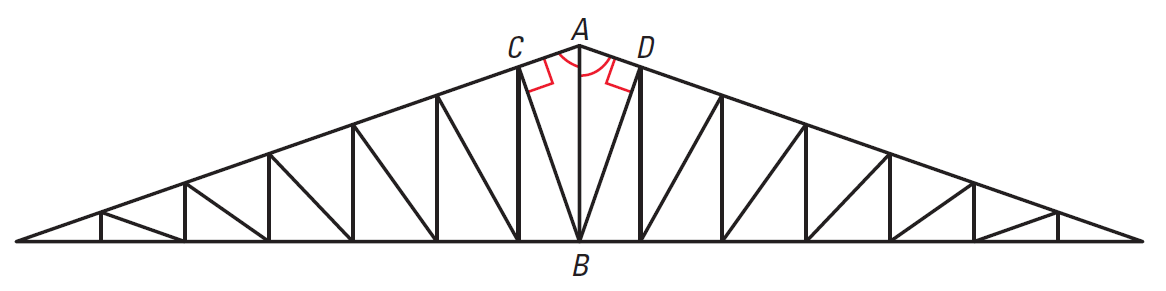
Answers

1. Answer :

(a) What segment lengths in the diagram are equal?

(b) Explain why Q is on MN?

Part (a) :

MN bisects ST, so NS = NT.

Because M is on the perpendicular bisector of ST, by Perpendicular Bisector Theorem,

MS = MT

The diagram shows that QS = QT = 12.

Part (b) :

QS = QT, so Q is equidistant from S and T.

By Converse of the Perpendicular Bisector Theorem Q is on the perpendicular bisector of ST, which is MN.

2. Answer :

Given :

D is on the bisector of ∠BAC, DB ⊥ AB, DC ⊥ AC

To Prove :

DB = DC

Plane for Proof :

Prove that ΔADB ≅ ΔADC.

Then conclude that DB ≅ DC, so DB = DC.

Proof :

By the definition of an angle bisector, ∠BAD ≅ ∠CAD.

Because ∠ABD and ∠ACD are right angles,

∠ABD ≅ ∠ACD

By the Reflexive Property of Congruence, AD ≅ AD.

By the AAS congruence theorem,

ΔADB ≅ ΔADC

Because corresponding parts of congruent triangles are congruent,

DB ≅ DC

By the definition of congruent segments,

DB = DC

3. Answer :

Because BC and BD meet AC and AD at right angles, they are perpendicular segments to the sides of ∠CAD.

This implies that their lengths represent the distances from the point B to AC and AD.

Because point B is on the bisector of ∠CAD, it is equidistant from the sides of the angle.

So, BC = BD, and you can conclude that So,

BC ≅ BD

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.