PIECEWISE DEFINED FUNCTIONS WORKSHEET

Problem 1 :

If f(x)  =  |x - 2|, then redefine f(x) as a piecewise function. 

Problem 2 :

Graph the piecewise-defined function shown below :

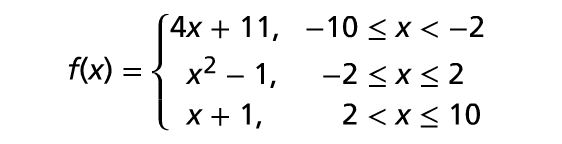
Problem 3 :

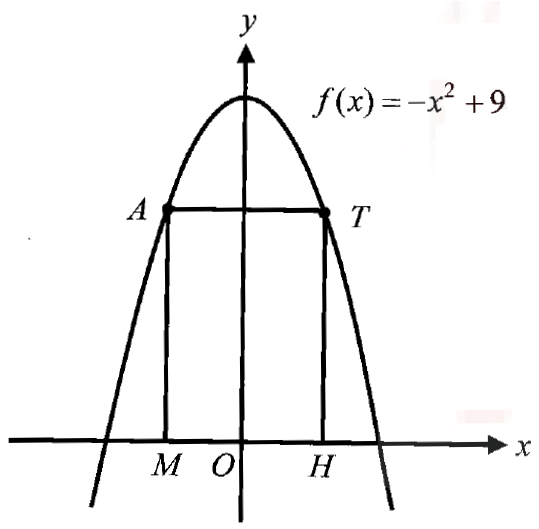
What is the rule that describes the piecewise-defined function shown in the graph ? 

Answers

Problem 1 :

If f(x)  =  |x - 2|, then redefine f(x) as a piecewise function. 

Solution : 

Take the stuff inside the absolute value and equate it to zero. 

x - 2  =  0 

x  =  2

From x  =  2, we can set three conditions as shown below. 

x < 2,  x = 2,  x > 2 

Case (i) : 

When x  <  2,

(x - 2)  <  0

So, we have

f(x)  =  -  (x - 2)

f(x)  =  - x + 2

f(x)  =  2 - x

Case (ii) : 

When x  =  0,

(x - 2)  =  0

So, we have

f(x)  =  0

Case (iii) : 

When x  >  2,

(x - 2)  >  0

So, we have

f(x)  =  x - 2

Hence, the given absolute value function is redefined as piecewise function as shown below :   

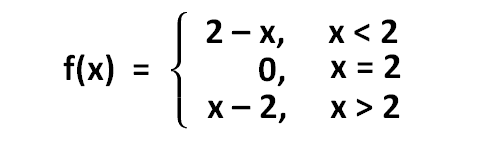
Problem 2 :

Graph the piecewise-defined function shown below :

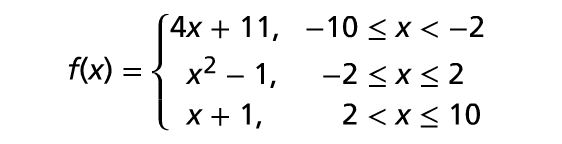
What are the domain and range ? Over what intervals is the function increasing or decreasing ?

Solution :

Step 1 :

Sketch the graph of y  =  4x + 11 for values of x between -10 and -2.

We can consider the following points to sketch the graph of y  =  4x + 11 : 

*  y = 4x + 11 is a linear equation. Then, its graph will be a straight line. 

*  y = 4x + 11 is in slope intercept form y = mx + b.

*  Comparing

y = 4x + 11 and y = mx + b 

we get a positive slope m = 4.

So, the graph of y = 4x + 11 is a rising line. 

Step 2 :

Sketch the graph of y = x² - 1 for values of x between -2 and 2.

We can consider the following points to sketch the graph of y = x² - 1 : 

*  y = x² - 1 is a quadratic equation. Then, its graph will be a parabola.  

*  The sign of x²  in y = x² - 1 is positive. So, the graph will be a open upward parabola. 

*  We can write y = x² - 1 in vertex form as shown below. 

y = (x - 0)² - 1

*  Comparing

y = (x - h)² + k  and  y = (x - 0)² - 1

we get the vertex (h, k)  =  (0, -1)

So, the graph of y = x² - 1 is a open upward parabola with the vertex (0, -1). 

Step 3 :

Sketch the graph of y  =  x + 1 for values of x between 2 and 10.

We can consider the following points to sketch the graph of y  =  x + 1 : 

*  y = x + 1 is a linear equation. Then, its graph will be a straight line. 

*  y = x + 1 is in slope intercept form y = mx + b.

*  Comparing

y = x + 1 and y = mx + b 

we get a positive slope m = 1.

So, the graph of y = x + 1 is a rising line. 

Graph :

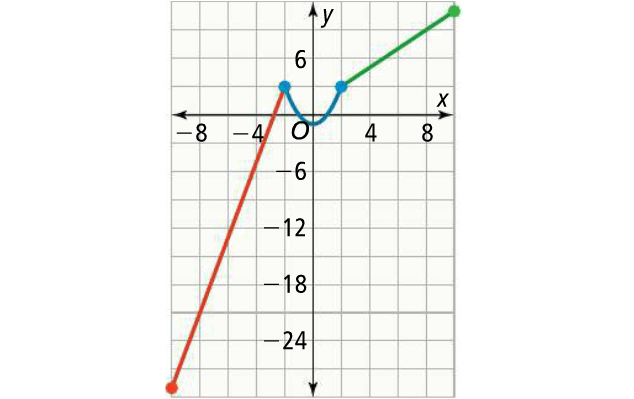
Domain and Range : 

To determine the range, calculate the y-values that correspond to the minimum and maximum x-values on the graph. 

For this graph, these values occur at the endpoints of the domain of the piecewise function,

-10 ≤ x ≤ 10

So, the domain is {x | -10 ≤ x ≤ 10}.

Evaluate y = 4x + 11 for x = -10 :

y  =  4(-10) + 11

y  =  - 40 + 11

y  =  - 29

Evaluate y = x + 1 for x = 10 :

y  =  10 + 1

y  =  11

So, the range is {y | -29 ≤ x ≤ 11}.

Increasing and Decreasing Intervals : 

The function is increasing when

- 10 < x < -2  and 0 < x < 10

The function is decreasing when

- 2 < x < 0

Problem 3 :

What is the rule that describes the piecewise-defined function shown in the graph ? 

Solution : 

Step 1 : 

Notice three separate linear pieces that make up the function. 

Step 2 : 

Determine the domain of each segment.

Step 3 : 

For each segment, use the graph to locate points on the line and to find the slope. 

Step 4 : 

We can use the slope-intercept form of a linear equation

f(x)  =  mx + b

to define the function of each segment. 

The rule for this function is :

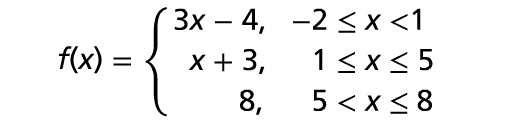
Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.