PLOT THE GIVEN POINTS ON THE CARTESIAN PLANE
Example 1 :
State the coordinates of the points J, K, L, M and N :
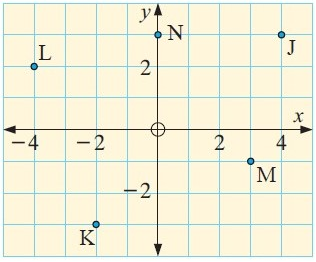
Solution :
From the Cartesian plane, we find the coordinates of the points J, K, L, M, and N.
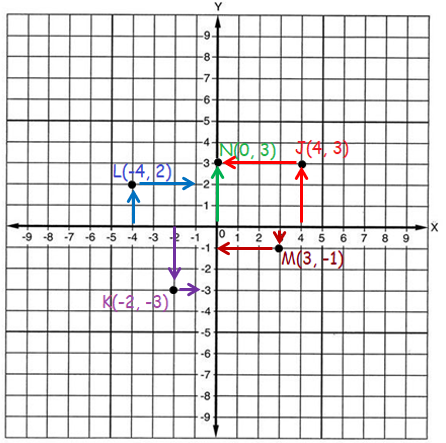
So, the Coordinates of points are J(4, 3), K(-2, -3), L(-4, 2), M(3, -1), and N(0, 3)
Example 2 :
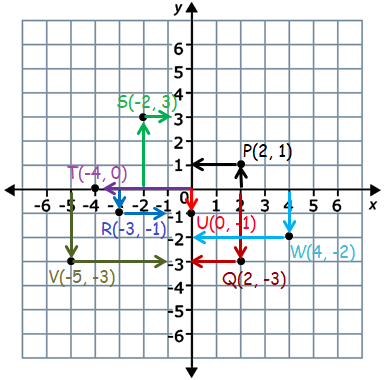
On the same set of axes plot the following points :
|
a. P(2, 1) b. Q(2, -3) c. R(-3, -1) d. S(-2, 3) |
e. T(-4, 0) f. U(0, -1) g. V(-5, -3) h. W(4, -2) |
Solution :
By plotting the given coordinates points on the Cartesian plane, we get
Example 3 :
If necessary, use Pythagoras’ Rule to find the distance between:
|
a. A and B b. C and D c. F and C d. F and A |
e. G and F f. A and D g. E and G h. E and D |
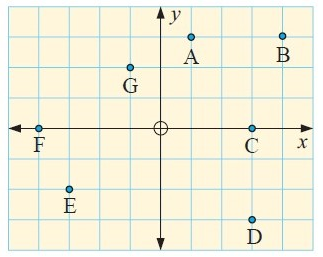
Solution :
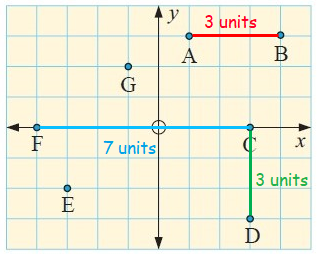
a.
By observing the graph, the distance between A and B is 3 units.
b.
By observing the graph, the distance between C and D is 3 units.
c.
By observing the graph, the distance between F and C is 7 units.
d.
In the figure, draw a horizontal segment of length 5 units from F and a vertical segment of length 3 units from A.
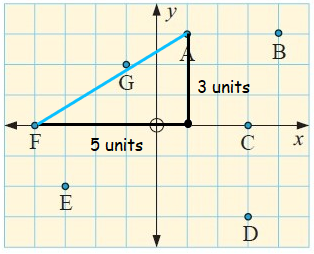
Using Pythagoras theorem :
a2 + b2 = c2
Here a = 3 units, b = 5 units and c = FA = ?
32 + 52 = c2
9 + 25 = c2
c2 = 34
FA = c = √34 units
So, the distance between F and A is √34 units.
e.
In the figure, draw a vertical segment of length 2 units from G and a horizontal segment of length 3 units from F.
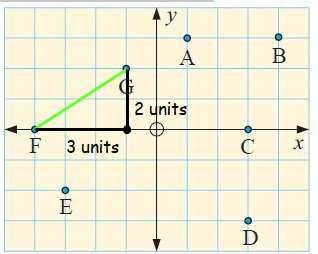
Using Pythagoras theorem :
a2 + b2 = c2
Here a = 2 units, b = 3 units and c = GF = ?
22 + 32 = c2
4 + 9 = c2
c2 = 13
GF = c = √13 units
So, the distance between G and F is √13 units.
f.
In the figure, draw a vertical segment of length 6 units from A and a horizontal segment of length 2 units from D.
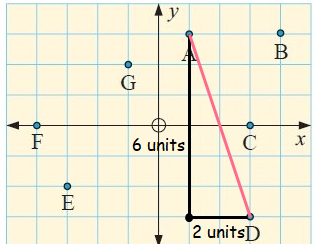
Using Pythagoras theorem :
a2 + b2 = c2
Here a = 6 units, b = 2 units and c = AD = ?
62 + 22 = c2
36 + 4 = c2
c2 = 40
c = √(10 × 4)
AD = c = 2√10 units
So, the distance between A and D is 2√10 units.
g.
In the figure, draw a horizontal segment of length 2 units from E and a vertical segment of length 4 units from G.
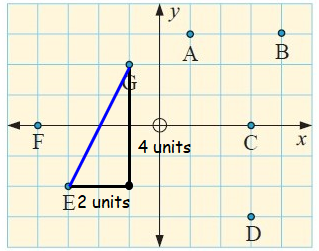
Using Pythagoras theorem :
a2 + b2 = c2
Here a = 4 units, b = 2 units and c = EG = ?
42 + 22 = c2
16 + 4 = c2
c2 = 20
c = √(5 × 4)
EG = c = 2√5 units
So, the distance between E and G is 2√5 units.
h.
In the figure, draw a horizontal segment of length 6 units from E and a vertical segment of length 1 unit from D.
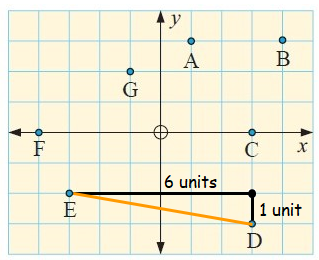
Using Pythagoras theorem :
a2 + b2 = c2
Here a = 6 units, b = 1 unit and c = ED = ?
62 + 12 = c2
36 + 1 = c2
c2 = 37
ED = c = √37 units
So, the distance between E and D is √37 units.
Example 4 :
Fill in the blanks:
(a) The point (3, 4) is at a distance of ___ units from x- axis and ___ units from y-axis.
(b) A point which lies on both the axes _________
(c) The x co-ordinate of a point lying on y axis is ____ and y co-ordinate of a point lying on x-axis is ____.
Solution :
(a) The point (3, 4) is at a distance of 3 units from x- axis and 4 units from y-axis.
(b) A point which lies on both the axes origin
(c) The x co-ordinate of a point lying on y axis is 0 and y co-ordinate of a point lying on x-axis is 0
Example 5 :
Write the ordinate of the given points:
(a) (3, 5)
(b) (4, 0)
(c) (2, 7)
Solution :
(a) (3, 5)
x-coordinate = 3
y-coordinate = 5
(b) (4, 0)
x-coordinate = 4
y-coordinate = 0
(c) (2, 7)
x-coordinate = 2
y-coordinate = 7
Example 6 :
Plot the given points on a graph sheet and check if the points lie on a straight line. If not, name the shape they form when joined in the given order
(1, 2), (2, 4), (3, 6) and (4, 8)
Solution :
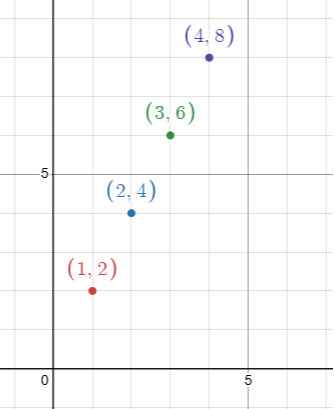
All the points lie on the same line.
Example 7 :
Plot a line graph for the variables p and q where p = 2q. Then, find:
(a) The value of p when q = 3
(b) The value of q when p = 8
Solution :
p = 2q
(a) when q = 3
p = 2(3)
p = 6
(b) when p = 8
8 = 2q
q = 8/2
q = 4
Example 8 :
Write the abscissa of the given points:
(a) (7, 3) (b) (5, 7) (c) (0, 5)
Solution :
abscissa is the x-coordinate.
(a) (7, 3) :
x-coordinate = 7
(b) (5, 7) :
x-coordinate = 5
(c) (0, 5) :
x-coordinate = 0
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
AP Calculus AB Problems with Solutions (Part - 10)
Feb 06, 25 09:46 AM
AP Calculus AB Problems with Solutions (Part - 10) -
AP Calculus AB Problems with Solutions (Part - 8)
Feb 05, 25 12:22 PM
AP Calculus AB Problems with Solutions (Part - 8) -
AP Calculus AB Problems with Solutions (Part - 9)
Feb 05, 25 12:15 PM
AP Calculus AB Problems with Solutions (Part - 9)
