PLOT THE GIVEN POLAR COORDINATE POINT IN THE POLAR COORDINATE SYSTEM

Polar Coordinate System :

A polar coordinate system is a plane with a point O, the pole  and ray from O the polar axis.

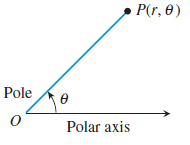
Each point P in the plane is assigned to polar coordinates

r is the directed distance from O to P and θ is the directed angle whose initial side is on the polar axis and whose terminal side is on the line OP.

As in trigonometry, we measure θ as positive when moving anticlockwise and negative when moving clockwise. 

If r > 0, then P is on the terminal side of θ. If r < 0 then P is on the terminal side of π + θ.

Example 1 :

Plot the points with the given polar coordinates.

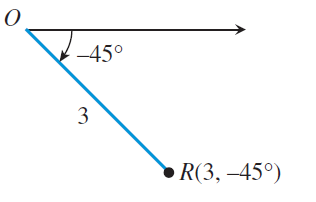
(a)  P(2, 2π/3)   (b)  Q(-1, 3π/4)    (c)  R(3, -45⁰)

Solution :

The given points has to be considered as (r, θ)

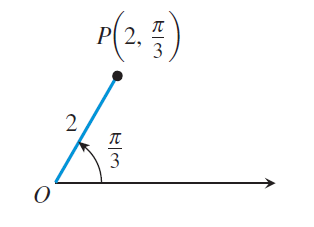
(a)  P(2, 2π/3)

Here r = 2 > 0 and θ  =  2π/3 (positive), so the terminal side is on P.

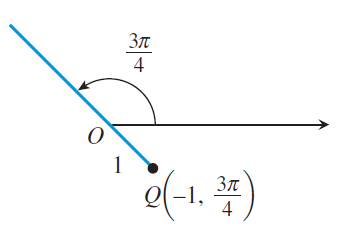
(b)  Q(-1, 3π/4)

Here r = -1 < 0 and θ  =  3π/4 (positive), so the point Q on the terminal side π + θ.

(c)  R(3, -45⁰)

Here r = 3 > 0 and θ  =  -45⁰ (negative), to get the terminal side we should have a anti clock wise rotation.

Note :

Each polar coordinates pair determines a unique point. However the polar coordinates of a point P in the plane are not unique.

Find all Polar Coordinates of a Point

Let P have polar coordinates (r, θ). Any other polar coordinate of P must be in the following form.

 (r, θ + 2nπ)  or (-r, θ + (2n + 1)π)

Where n is any integer. In particular, the pole has polar coordinates (0, θ), where θ is any angle.

Example :

Polar coordinates of P are given. Find all of its polar coordinates.

(i)  P(2, π/6)

(ii) P(2, -π/4)    

Solution :

(i)  P(2, π/6)

Here r  =  2  > 0 and θ  =  π/6

 (r, θ + 2nπ)  or (-r, θ + (2n + 1)π)

 (2, π/6 + 2nπ)  or (-2, π/6 + (2n + 1)π)

Where n is an integer.

(ii)   P(2, -π/4) 

Here r  =  2  > 0 and θ  =  -π/4

 (r, θ + 2nπ)  or (-r, θ + (2n + 1)π)

 (2, -π/4 + 2nπ)  or (-2, -π/4 + (2n + 1)π)

Where n is an integer.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.