POINT LINE LINE SEGMENT RAY AND PLANE
Point
Point is not something new to us. Many graphs are being drawn using points.
A point is smaller than a tip of a pencil or pen used by us. Therefore a point has not length, width, height or thickness.
A point indicates a definite position.
Points are usually denoted by capital letters A, B, C and so on as given below.

Line
Observe the figure given below carefully.
As the space in between the points decreases they join to form a line. A line is a set of points closely arranged without gap.
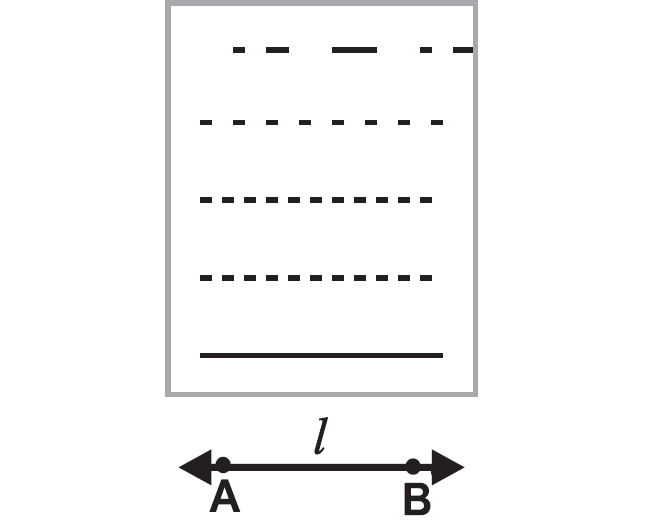
Mark A, B on a sheet of paper using a scale and draw a line passing through these points.
This is a straight line.
It is represented as straight line AB or line "l".
When we represent a straight line as AB, it means,
(i) The line passes through the points A and B.
(ii) The line extends on either side of A and B.
Observe the names given for the following straight lines.
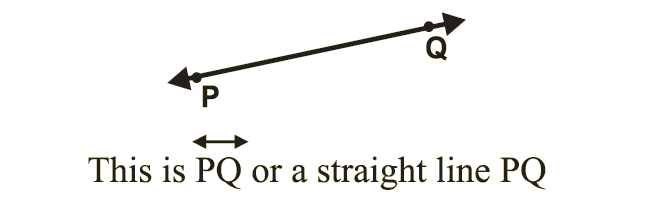
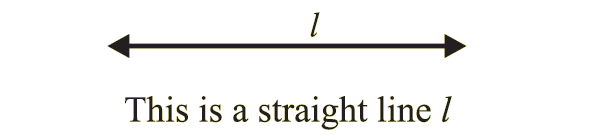
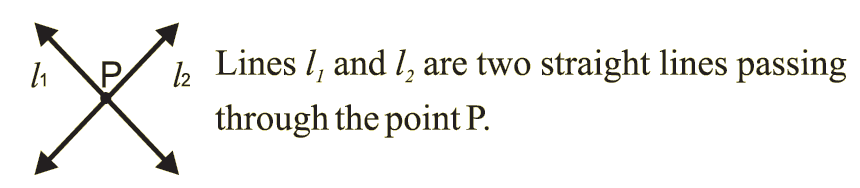
Ray
A ray starts from a fixed point and extends indefinitely in other direction.

1. Starting point of the ray is A.
2. The ray passes through the points A and B.
3. The ray extends through the point B.
A ray is a straight line with a starting point and extends indefinitely in one direction.
Line Segment
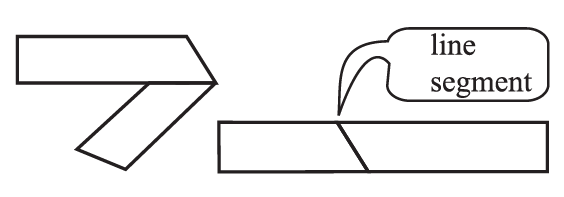
If a sheet of paper is folded and then opened, the folded part represents the line segment.
It is shown in the figure given below.
Mark X, Y and Z on the straight line AB.

Consider AX a part of the straight line, which starts at A and ends at X. So, it has a particular length. This is called a line segment. It can be denoted as line segment AX.
Few more line segments from the above figure are AY, AB, XY, XB, YB, XZ.
Therefore line segment is a part of a line. It has a starting point and end point.
A line segment has definite length.
Plane
Straight lines, points and rays can be represented in a sheet of paper or on the black board. Isn't it ?
Likewise floor, wall, black board, card board and top portion of the table are few examples of plane.
A plane is a flat surface which extends indefinitely in all directions as given in the figure given below.

How many points are required to form a plane ?
It is enough to have three points that do not lie on the same straight line.
Relation between Points and Lines
Collinear Points :
1. Check whether you can draw a straight line passing through the points A and B.

2. Check whether you can draw a straight line passing through the points A, B and C.

3. Check whether you can draw a straight line passing through the points P, Q and C.
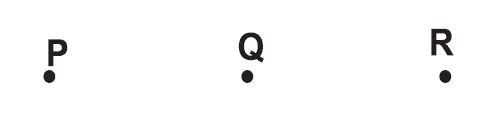
Answers :
1. You can draw a straight line passing through the two points A and B.
2. Since A, B and C are not on the same straight line, a straight line can not be drawn through A, B and C.
3. A straight line can be drawn through P, Q and R, as they lie on the same straight line.
So, P, Q and R are collinear points.
Hence, the following statements are true.
(i) A straight line can be drawn through any two given points.
(ii) It is not always possible to draw a straight line passing through any 3 points.
(iii) But a straight line can be drawn passing through 3 collinear points.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Permutation Problems with Solutions
May 08, 25 12:28 PM
Permutation Problems with Solutions -
Digital SAT Math Problems and Solutions (Part - 159)
May 08, 25 01:39 AM
Digital SAT Math Problems and Solutions (Part - 159) -
Digital SAT Math Problems and Solutions (Part - 158)
May 06, 25 11:00 AM
Digital SAT Math Problems and Solutions (Part - 158)