POINT OF CONCURRENCY IN A TRIANGLE

There are four points of concurrency in a triangle.

They are

Centroid

Incenter

Circumcenter

Orthocenter

Key Concept :

A point of concurrency is the point where three or more line segments or rays intersect. 

Let us discuss the above four points of concurrency in a triangle in detail. 

Centroid

The point of concurrency of the medians of a triangle is called the centroid of the triangle and is usually denoted by G.

Important points - Centroid

1. Three medians can be drawn in a triangle.

2. The centroid divides a median in the ratio 2:1 from the vertex.

3. The centroid of any triangle always lie inside the triangle.

Incenter

The point of concurrency of the internal angle bisectors of a triangle is called the incenter of the triangle and is denoted by I.

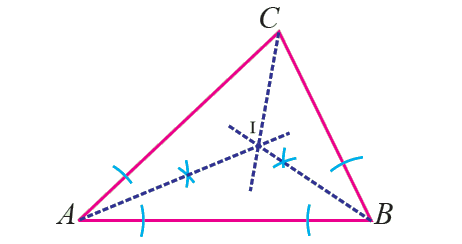
Points to Remember - Incenter

1. Three internal angle bisectors can be drawn in a triangle.

2. Each internal angle bisector will divide the vertex angle into two equal parts. 

3. The incenter of any triangle always lies inside the triangle.

Circumcenter

The point of concurrency of the perpendicular bisectors of the sides of a triangle is called the circumcenter and is usually denoted by S.

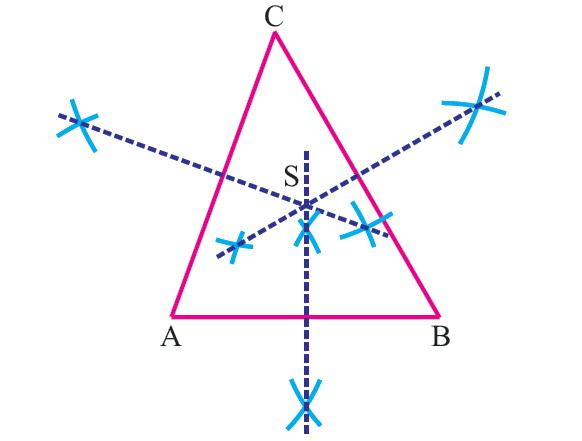
Points to Remember - Circumcenter

1. The circumcenter of an acute angled triangle lies inside the triangle.

2. The circumcenter of a right triangle is at the midpoint of its hypotenuse.

3. The circumcenter of an obtuse angled triangle lies outside the triangle.

Orthocenter

The point of concurrency of the altitudes of a triangle is called the orthocenter of the triangle and is usually denoted by H.

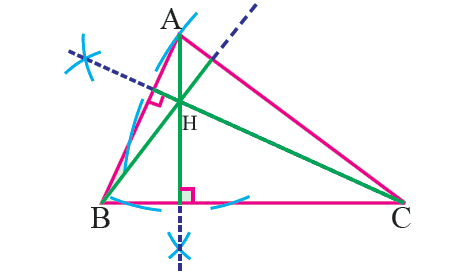
Points to Remember - Orthocenter

1. Three altitudes can be drawn in a triangle.

2. The orthocenter of an acute angled triangle lies inside the triangle.

3. The orthocenter of a right triangle is the vertex of the right angle.

4. The orthocenter of an obtuse angled triangle lies outside the triangle.

Problem 1 :

Points S, T and U are the midpoints of DE, EF and DF respectively. Find x, y and z.

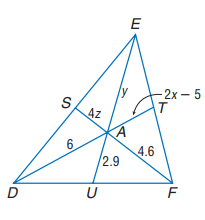
Solution :

Finding the value of x :

DT = DA + AT

DT = 6 + 2x - 5

= 2x + 1

DA = 2/3 of DT

6 = (2/3) (2x + 1)

3(6) = 2(2x + 1)

18 = 4x + 2

18 - 2 = 4x 

4x = 16

x = 16/4

x = 4

Finding the value of y :

EA = y, EU = EA + AU

EU = y + 2.9

EA = 2/3 of EU

y = (2/3) (y + 2.9)

3y = 2(y + 2.9)

3y = 2y + 5.8

3y - 2y = 5.8

y = 5.8

Finding the value of z :

FA = 2/3 FS

FS = FA + AS

= 4.6 + 4z

By applying the value of FS, we get

4.6 = 2/3 of (4.6 + 4z)

4.6 = (2/3)(4.6 + 4z)

3(4.6) = 2(4.6 + 4z)

13.8 = 9.2 + 8z

13.8 - 9.2 = 8z

4.6 = 8z

z = 4.6/8

z = 0.575

Problem 2 :

In the diagram, the perpendicular bisectors (shown with dashed segments) of MBC meet at point G-the circumcenter. and are shown dashed. Find the indicated measure.

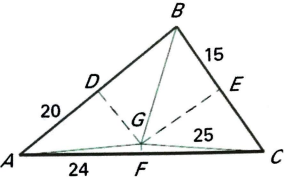
a)  AG =

b) BD =

c) CF =

d) CE = ----

e)  AB = ----

f)  AC = ----

g) m <ADG = ----

h) If BG = (2x- 15), find x.

Solution :

In triangle GFC,

GC² = GF² + FC²

FC = 24 (because GF is perpendicular bisector)

25² = GF² + 24²

625 = GF² + 576

GF² = 625 - 576

GF² = 49

GF = 7

a) Then AG = 25

b)  BD = 20

DG is the perpendicular bisector of AB.

c) CF = 24

d)  CE = 15 (BE = CE)

e)  AB = AD + DB

= 20 + 20

AB = 40

f)  AC = AF + FC

= 24 + 24

AC = 48

g) m <ADG = 90 degree

Because DG, GF and GE are perpendicular bisectors.

h) If BG = (2x- 15)

In triangle DGB,

BG = AG = GC

BG = 25

2x - 15 = 25

2x = 25 + 15

2x = 30

x = 30/2

x = 15

So, the value of x is 15.

Problem 3 :

In the diagram, the perpendicular bisectors (shown with dashed segments) of triangle MNP meet at point 0-the circumcenter. Find the indicated measure.

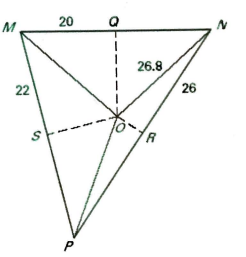
a. MO = ___

b. PR = ___

c. MN = ----

d. SP = __

e. m<MQO = __

f. If OP = 2x, find x.

Solution :

a) Since ON = 26.8, then MO = 26.8

b)  Since RN = 26, then PR = 26

c)  MN = MQ + QN

Since OQ is the perpendicular bisector, MQ and QN are equal

MN = 20 + 20

MN = 40

d) SP = MS = 22

e. m<MQO = 90 degree

f. If OP = 2x

26.8 = 2x

x = 26.8/2

x = 13.4

Related Topics

Construction of centroid

Construction of incenter

Construction of circumcenter

Construction of orthocenter

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.