POINT OF CONCURRENCY WORKSHEET

Questions 1-4 : Choose the letter with the name of the segment/line/ray shown.

Question 1 :

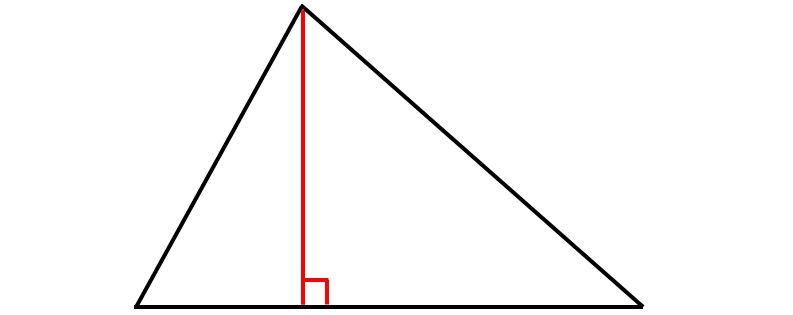
(a) perpendicular bisector

(b) angle bisector 

(c) median

(d) altitude

Question 2 :

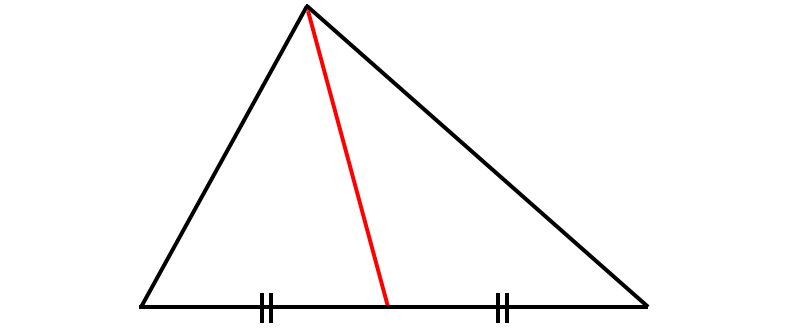
(a) perpendicular bisector

(b) angle bisector 

(c) median

(d) altitude

Question 3 :

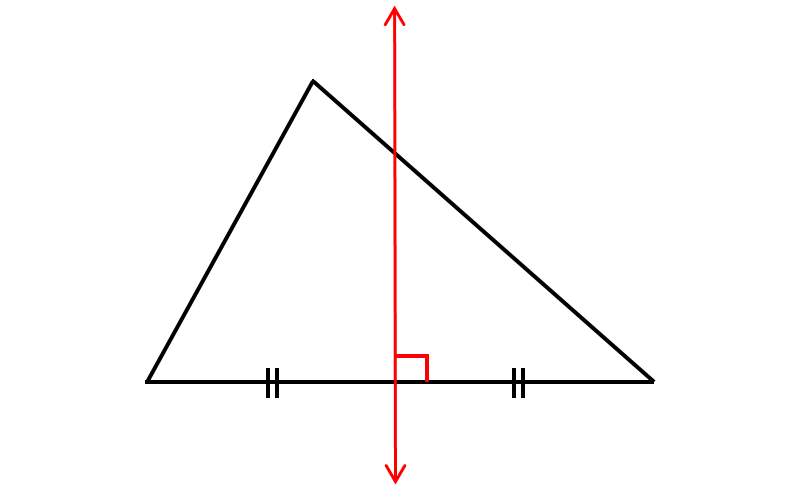
(a) perpendicular bisector

(b) angle bisector 

(c) median

(d) altitude

Question 4 :

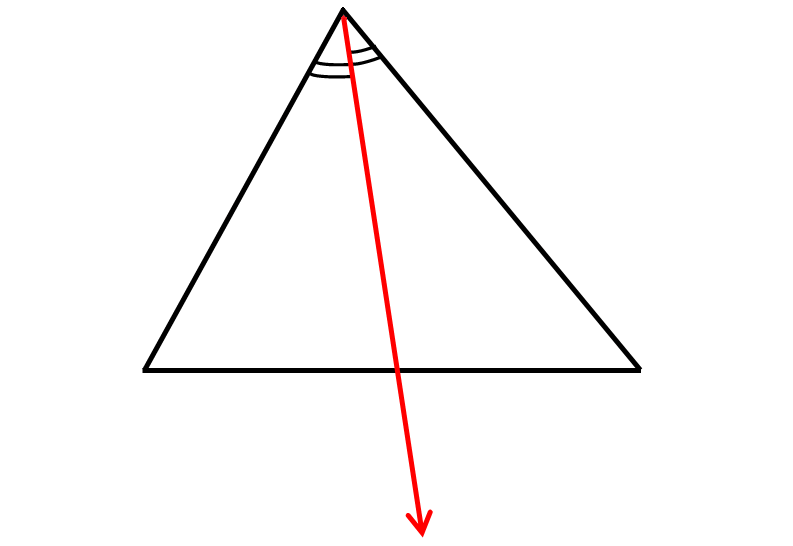
(a) perpendicular bisector

(b) angle bisector 

(c) median

(d) altitude

Questions 5-11 : Choose the letter with the name of the correct point of concurrency.

Question 5 :

The point of intersection of the three altitudes of a triangle :

(a) circumcenter 

(b) incenter 

(c) centroid

(d) orthocenter

Question 6 :

The point of intersection of the three medians of a triangle :

(a) circumcenter 

(b) incenter 

(c) centroid

(d) orthocenter

Question 7 :

The point of intersection of the three perpendicular bisectors of a triangle :

(a) circumcenter 

(b) incenter 

(c) centroid

(d) orthocenter

Question 8 :

The point of intersection of the three angle bisectors of a triangle :

(a) circumcenter 

(b) incenter 

(c) centroid

(d) orthocenter

Question 9

It is equidistant from the three vertices of a triangle :

(a) circumcenter 

(b) incenter 

(c) centroid

(d) orthocenter

Question 10 :

It is equidistant from the three sides of a triangle :

(a) circumcenter 

(b) incenter 

(c) centroid

(d) orthocenter

Question 11 :

It divides each median into two sections at a 2 : 1 ratio :

(a) circumcenter 

(b) incenter 

(c) centroid

(d) orthocenter

Questions 12-18 : Name the point of concurrency shown.

Question 12 :

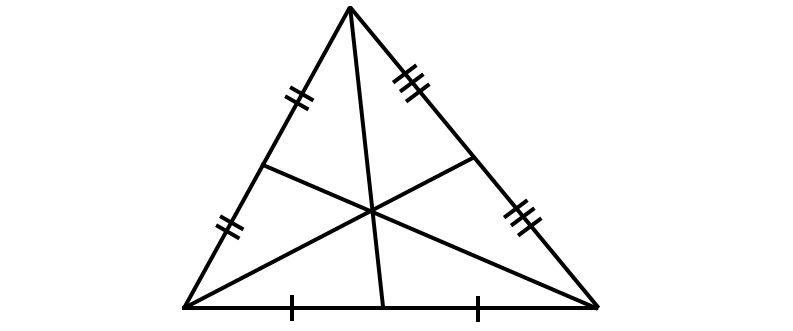
Question 13 :

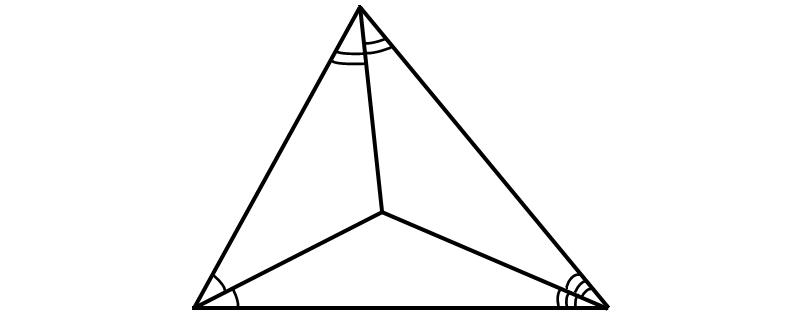
Question 14 :

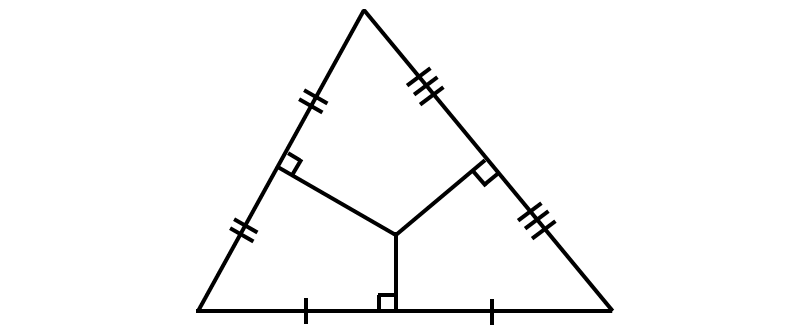
Question 15 :

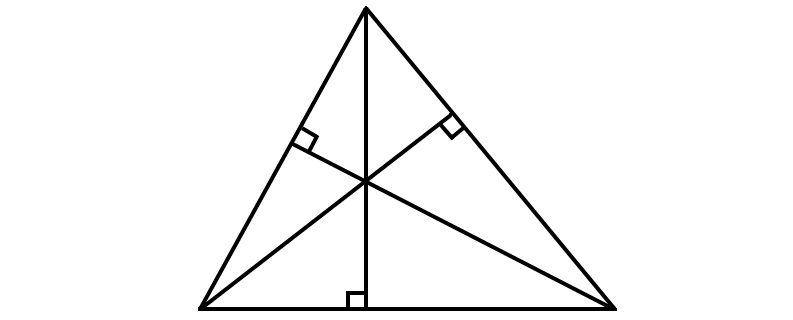
Question 16 :

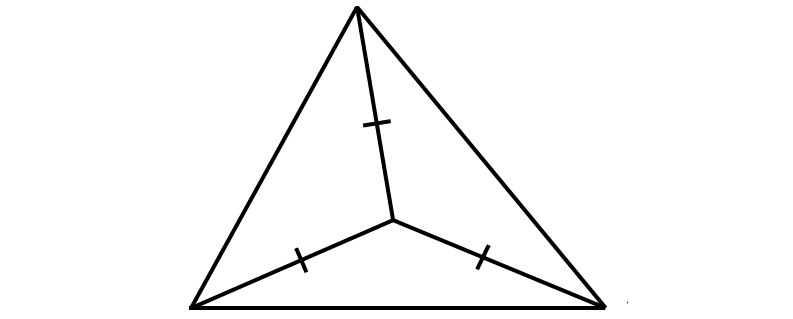
Question 17 :

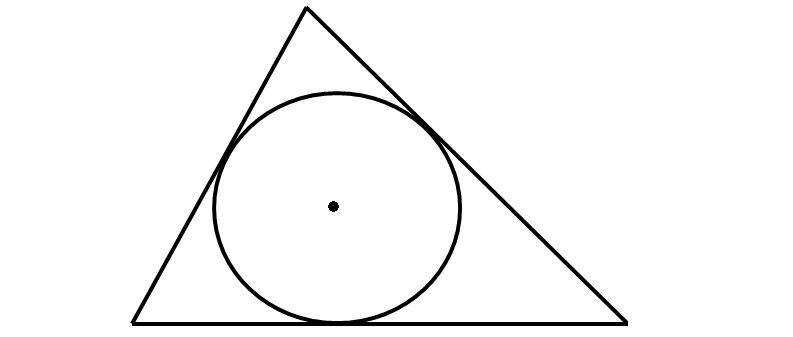
Question 18 :

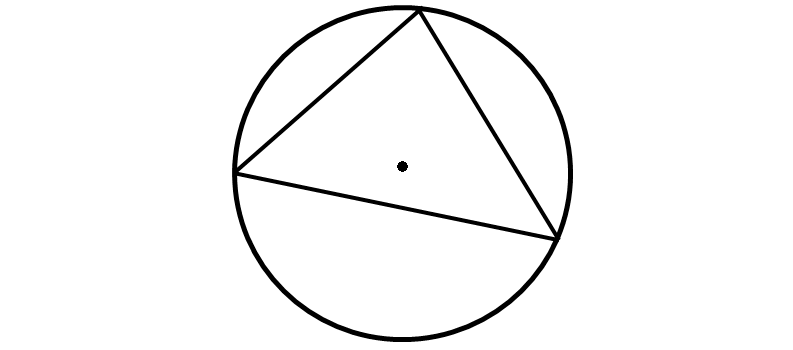
Question 19 :

Which of the following can be used to inscribe a circle about a triangle. 

(a) circumcenter 

(b) incenter 

(c) centroid

(d) orthocenter

Question 20 :

Which of the following can be used to circumscribe a circle about a triangle. 3

(a) circumcenter 

(b) incenter 

(c) centroid

(d) orthocenter

Answers

1.  (d) altitude

2.  (c) median

3.  (a) perpendicular bisector 

4.  (b) angle bisector

5.  (d) orthocenter

6.  (c) centroid

7.  (a) circumcenter

8.  (b) incenter

9.  (a) circumcenter

10.  (b) incenter

11.  (c) centroid

12.  centroid

13.  incenter

14.  circumcenter

15.  orthocenter

16.  circumcenter

17.  incenter

18.  circumcenter

19.  incenter

20.  circumcenter

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.