POLAR FORM TO STANDARD FORM AND STANDARD FORM TO POLAR FORM EXAMPLES

What is complex number ?

A complex number is the sum of a real number and an imaginary number. 

Standard form :

z  =  a + ib

Its represented by ‘z’.

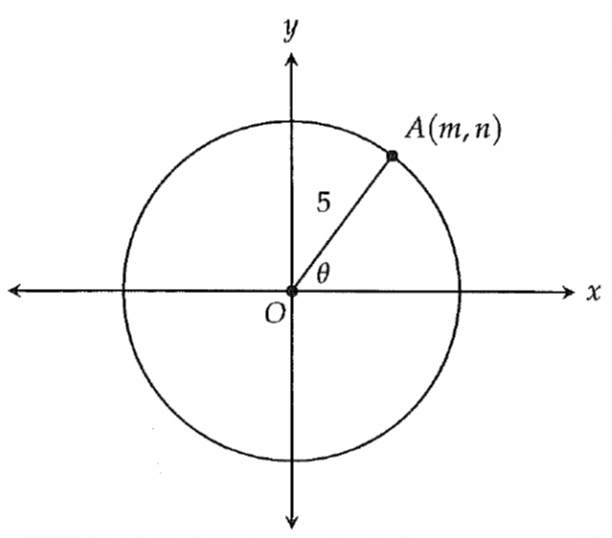
What is polar form ?

The complex number a + bi is written in polar form as,

z  =  r(cos θ + i sin θ)

(where a  =  r cos θ, and b  =  r sin θ)

The value of r is called the modulus of a complex number z. i.e, r  =  |z|

To find the r, we use the formula r  =  √(a² + b²).

The angle θ is called the argument of the complex number z. i.e, θ  =  arg(z). 

To find the arg(z), we will use α  =  tan^-1|b/a|.

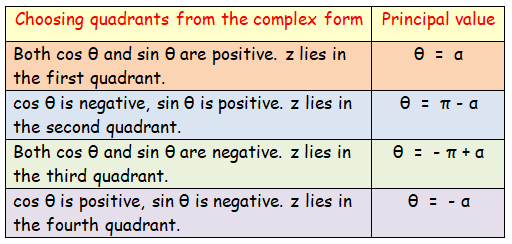
To find the principal value θ of a complex number, we may use the following methods.

Write the complex number in standard form :

Example 1 :

3(cos 30˚ - i sin 30˚)

Solution :

Given, z  =  3(cos 30˚ - i sin 30˚)

By using the calculator, we get

z  =  3[√3/2 - i(1/2)]

z  =  3√3/2 - 3/2i

So, the standard form is 3√3/2 - 3/2i.

Example 2 :

8(cos 210˚ + i sin 210˚)

Solution :

Given, z  =  8(cos 210˚ + i sin 210˚)

By using the calculator, we get

z  =  8[-√3/2 + i(-1/2)]

z  =  (-8√3/2) - (8/2i)

z  =  -4√3 - 4i

So, the standard form is -4√3 - 4i.

Example 3 :

√7(cos π/12 + i sin π/12)

Solution :

Given, z  =  √7(cos π/12 + i sin π/12)

By using the calculator, we get

z  =  √7[((√6 + √2)/4) + i((√6 - √2)/4)]

z  =  √7[(√6 + √2)/4] + √7[(√6 - √2)/4]i

So, the standard form is 

√7[(√6 + √2)/4] + √7[(√6 - √2)/4]i

Write the complex number to polar form :

Example 4 :

2 + 2i

Solution :

Given, z  =  2 + 2i

2 + 2i  =  r(cos θ + i sin θ) -----(1)

Since the complex number 2 + 2i is positive, z lies in the first quadrant.

So, the principal value θ  =  π/4

By applying the value of r and θ in equation (1), we get

2 + 2i  =  2√2(cos π/4 + i sin π/4)

So, the polar form of the complex number z is

2√2(cos π/4 + i sin π/4)

Example 5 :

-2i

Solution :

Given, z  =  0 - 2i

0 - 2i  =  r(cos θ + i sin θ) -----(1)

Since the complex number 0 - 2i is positive and negative, z lies in the fourth quadrant.

So, the principal value θ  =  - π/2

By applying the value of r and θ in equation (1), we get

0 – 2i  =  2(cos (-π/2) + i sin (-π/2))

So, the polar form of z is 2(cos (-π/2) + i sin (-π/2))

Example 6 :

√3 + i

Solution :

Given, z  =  √3 + i

√3 + i  =  r(cos θ + i sin θ) -----(1)

Since the complex number √3 + i has a positive, z lies in the first quadrant.

So, the principal value θ  =  π/6

By applying the value of r and θ in equation (1), we get

√3 + i  =  2(cos π/6 + i sin π/6)

So, the polar form of z is 2(cos π/6 + i sin π/6)

Apart from the stuff given above,  if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.