POLYNOMIAL WORD PROBLEMS WITH PERIMETER AND AREA

Problem 1 :

In the picture shown below, set up an equation and hence find the value of x and find the area.

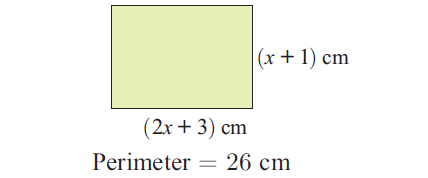
Solution :

Perimeter = 26

Sum of the lengths of all sides = 26

(2x + 3) + (x + 1) + (2x + 3) + (x + 1) = 26

2x + x + 2x + x + 3 + 1 + 3 + 1 = 26

6x + 8 = 26

6x = 18

x = 3

Area of rectangle :

= length x width

= 9 x 4

= 36 cm²

Problem 2 :

Find the value of x.

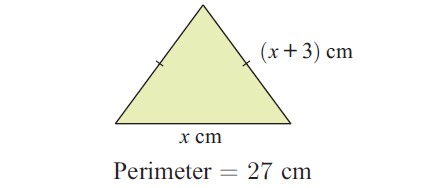
Solution :

Perimeter of the triangle = 27

From the picture it is a isosceles triangle, so two sides will be equal.

x + (x + 3) + (x + 3) = 27

x + x + 3 + x + 3 = 27

3x + 6 = 27

3x = 21

x = 7

Problem 3 :

Find x, given that the square and the rectangle have equal areas.

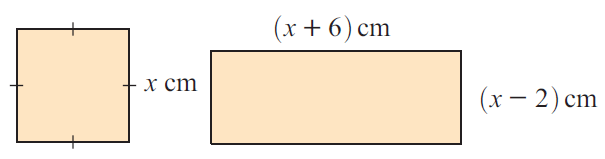
Solution :

Area of square = Area of rectangle

x² = (x + 6)(x - 2)

x² = x² - 2x + 6x - 12

0 = 4x - 12

4x = 12

x = 3

Problem 4 :

A rectangular paddock has a length 300 m greater than its width. If the perimeter of the paddock is 1400 m, find:

(a) the width (b) the length.

Solution :

Let x be the width.

Length = x + 300

Perimeter of the paddock = 1400

2(length + width) = 1400

2(x + x + 300) = 1400

2(2x + 300) = 1400

2x + 300 = 700

2x = 400

x = 200

So, width of the rectangle is 200 m and length of the rectangle is 500 m.

Problem 5 :

The length of the rectangle is 11 cm more than its width, the area of the rectangle is 2040 cm². Find the dimension of the rectangle.

Solution :

Let x be the width.

Length = x + 11

Area of the rectangle = 2040

length x width = 2040

x(x + 11) = 2040

x² + 11x - 2040 = 0

(x + 51)(x - 40) = 0

x = -51  or  x = 40

Since x represents width of the rectangle, it can not be a negative value.

So,

x = 40

That is,

width = 40 cm

length = 40 + 11 = 51 cm

Problem 6 :

The perimeter of this pentagon is 70 units.

a What is the value of x?

b What is the length of the shortest side?

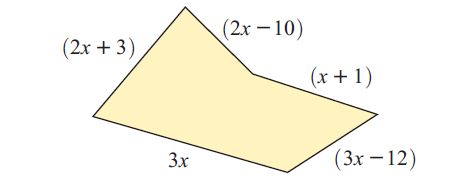
Solution :

Perimeter of the pentagon = 70

3x + 2x + 3 + 2x - 10 + x + 1 + 3x - 12 = 70

11x - 18 = 70

11x = 88

x = 8

Longest side :

= 3(8)

= 24 units

Shortest side :

= 2(8) - 10

= 16 - 10

= 6 units

Problem 7 :

The isosceles triangle illustrated has a base of length 18 cm.

a) What is the value of x?

b) Is the triangle equilateral? Explain your answer.

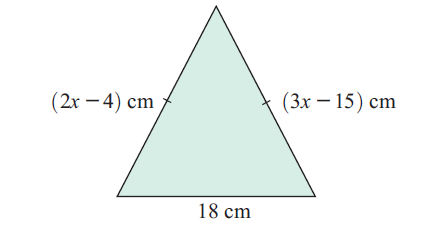
Solution :

From the triangle shown above,

2x - 4 = 3x - 15

2x - 3x = -15 + 4

-x = -11

x = 11

Substitute x = 11 in 2x - 4.

= 2(11) - 4

= 22 - 4

= 18 cm

Substitute x = 11 in 3x - 15.

= 3(11) - 15

= 33 - 15

= 18 cm

Since the length of all sides are equal, it is a equilateral triangle.

Problem 8 :

Adjacent sides of a rhombus have lengths (2x + 11) cm and (4x + 5) cm. Find x and hence find the perimeter of the rhombus.

Solution :

In rhombus, all the four sides are equal in length.

2x + 11 = 4x + 5

2x - 4x = 5 - 11

-2x = -6

x = 3

Perimeter of the rhombus = 2(2x + 11 + 4x + 5)

=  2(6x + 16)

= 12x + 32

Substitute x = 3.

= 12(3) + 32

= 36 + 32

= 68 cm

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.