POWERS OF 10 AND SCIENTIFIC NOTATION

Powers of 10

Powers of 10 can be used to read and write very large and very small numbers, such as the masses of atomic particles. 

The table shows the relationship between several powers of 10. 

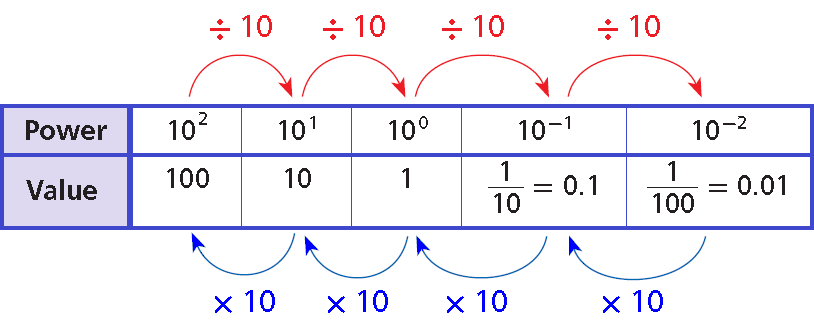
• Each time you divide by 10, the exponent decreases by 1 and the decimal point moves one place to the left. 

• Each time you multiply by 10, the exponent increases by 1 and the decimal point moves one place to the right. 

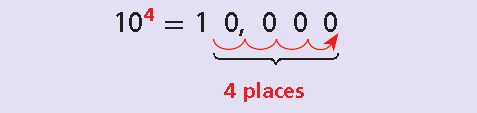
Positive Integer Exponent :

If n is a positive integer, find the value of 10ⁿ by starting with 1 and moving the decimal point n places to the right. 

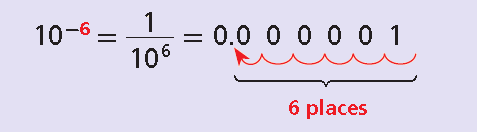
Negative Integer Exponent :

If n is a positive integer, find the value of 10^-n by starting with 1 and moving the decimal point n places to the left. 

Evaluating Powers of 10

Example 1 : 

Find the value : 

10^-3

Solution :

=  10^-3

The exponent is negative 3. So, start with 1 and move the decimal point three places to the left.

=  0.001

Example 2 : 

Find the value : 

10²

Solution :

=  10²

The exponent is positive 2. So, start with 1 and move the decimal point two places to the right.

=  100

Example 3 : 

Find the value : 

10⁰

Solution :

=  10⁰

The exponent is zero. So, start with 1 and move the decimal point zero places. 

=  1

Writing Powers of 10

Example 4 : 

Write the following number as a power of 10.

10,000,000

Solution :

=  10,000,000

The decimal point is seven places to the right of 1.

So, the exponent is 7.

=  10⁷

Example 5 : 

Write the following number as a power of 10.

0.001

Solution :

=  0.001

The decimal point is three places to the left of 1.

So, the exponent is -3.

=  10^-3

Example 6 : 

Find the value : 

10

Solution :

=  10

The decimal point is one place to the right of 1.

So, the exponent is 1.

=  10¹

Note : 

We can also move the decimal point to find the product of any number and a power of 10. We start with the number instead of starting with 1. 

Multiplying by Powers of 10

If the exponent is a positive integer, move the decimal point to the right.  

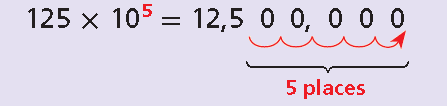
If the exponent is a negative integer, move the decimal point to the left.  

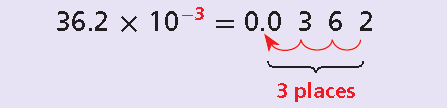
Example 7 : 

Find the value of the expression.

89.74 x 10⁶

Solution :

=  89.74 x 10⁶

The exponent is positive 6.

So, move the decimal point six places to the right.

=  89,740,000

Example 8 : 

Find the value of the expression.

28.4 x 10^-4

Solution :

=  28.4 x 10^-4

The exponent is negative 4.

So, move the decimal point four places to the left.

=  0.00284

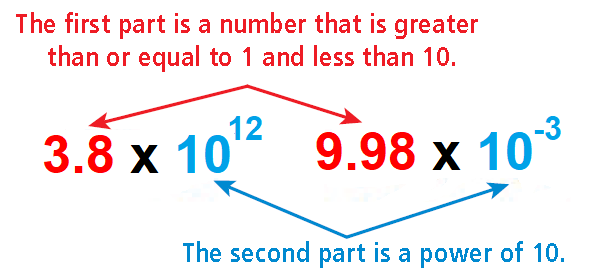
Scientific Notation

Scientific notation is a method of writing numbers that are very large or very small. A number written in scientific notation has two parts that are multiplied. 

Example 9 : 

Jupiter has a diameter of about 143,000 km. Its shortest distance from Earth is about 5.91 x 10⁸ km, and its average distance from the Sun is about 778,400,000 km. Jupiter's orbital speed is approximately 1.3 x 10⁴ m/s. 

(i) Write Jupiter's diameter in scientific notation.

(ii) Write Jupiter's shortest distance from Earth in standard form. 

(iii) Write Jupiter's average distance from the Sun in scientific notation. 

(iii) Write Jupiter's orbital speed in standard form. 

Solution :

Jupiter's diameter in scientific notation :

=  143,000

The decimal point has to be moved 5 places to the left to get a number between 1 and 10.

Then, 

=  1.43 x 10⁵ km

Jupiter's shortest distance from Earth in standard form :

=  5.91 x 10⁸

The exponent is positive 8.

So, move the decimal point eight places to the right.

=  591000000 km

Jupiter's average distance from the Sun in scientific notation :

=  778,400,000

The decimal point has to be moved 8 places to the left to get a number between 1 and 10.

Then, 

=  7.784 x 10⁸

Jupiter's orbital speed in standard form :

= 1.3 x 10⁴

The exponent is positive 4.

So, move the decimal point four places to the right.

=  13,000 m/s

Comparing and Ordering Numbers in Scientific Notation 

Example 10 :

Order the following list of numbers from least to greatest.

1.2x10^-1, 8.2x10⁴, 6.2x10⁵, 2.4x10⁵, 1x10^-1, 9.9x10^-4 

Solution :

Step 1 : 

List the numbers in order by powers of 10.

9.9x10^-4, 1.2x10^-1, 1x10^-1, 8.2x10⁴, 6.2x10⁵, 2.4x10⁵

Step 2 : 

Order the numbers that have the same powers of 10.

9.9x10^-4, 1x10^-1, 1.2x10^-1, 8.2x10⁴, 2.4x10⁵, 6.2x10⁵

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.