PRACTICAL PROBLEMS USING MIDPOINT FORMULA

Question 1 :

The points A(−3, 6) , B(0, 7) and C(1, 9) are the mid-points of the sides DE, EF and FD of a triangle DEF. Show that the quadrilateral ABCD is a parallelogram

Solution :

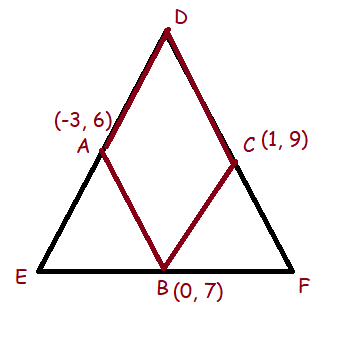
In order to prove ABCD is a parallelogram, we have to find the point D.

  =  D (-3+1-0, 6+9-7)

  =  D (-2, 8)

In ABCD is a parallelogram, then midpoint of diagonals AC and BD will be equal.

Midpoint of AC  =  (-3 + 1)/2, (6 + 9)/2

  =  -2/2, 15/2

  =  (-1, 15/2)

Midpoint of BD

B(0, 7) and D(-2, 8)

  =  (0 - 2)/2, (7 + 8)/2

  =  -2/2, 15/2

  =  (-1, 15/2)

Hence ABCD is a parallelogram.

Question 2 :

A (−3, 2) , B (3, 2) and C (−3, −2) are the vertices of the right triangle, right angled at A. Show that the mid-point of the hypotenuse is equidistant from the vertices.

Solution :

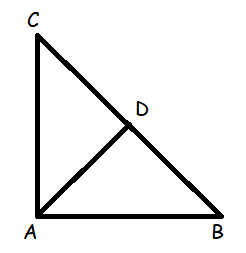
Mid point of BC  =  (3 + (-3))/2, (2 + (-2))/2

  = D (0, 0)

Distance between AD :

A(-3, 2) D(0, 0)

  =  √(x₂ - x₁)² + (y₂ - y₁)²

  =  √(-3-0)² + (2-0)²

  =  √9 + 4

  =  √13

C(-3, -2) D(0, 0)

  =  √(x₂ - x₁)² + (y₂ - y₁)²

  =  √(-3-0)² + (-2-0)²

  =  √9 + 4

  =  √13

B(3, 2) D(0, 0)

  =  √(x₂ - x₁)² + (y₂ - y₁)²

  =  √(0-3)² + (0-2)²

  =  √9 + 4

  =  √13

Hence the midpoint of the hypotenuse is equidistant from the vertices.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.