PRACTICAL PROBLEMS USING PYTHAGOREAN THEOREM

Problem 1 :

5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.

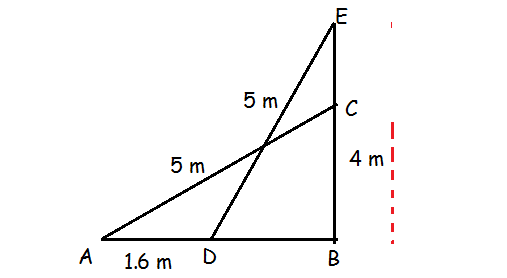
Solution :

In triangle ABC,

AC²  =  AB² + BC²

5²  =  AB² + 4²

AB²  =  25 - 16

AB²  =  9

AB  =  3

DB  =  AB - AD

DB  =  3 - 1.6

DB  =  1.4

In triangle DBE,

ED²  =  EB² + DB² 

5²  =  EB² + (1.4)² 

EB²  =  25 - 1.96

EB = √23.04

EB  =  4.8

EC  =  EB - BC

=  4.8 - 4

EC  =  0.8 m

So, the required distance is 0.8 m.

Problem 2 :

The perpendicular PS on the base QR of a triangle PQR intersects QR at S, such that QS = 3 SR. Prove that 2PQ² = 2PR² + QR²

Solution :

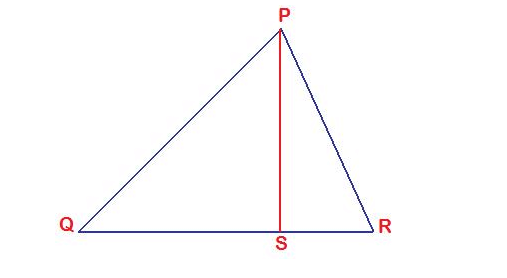
QR   =   QS + RS

QR   =   3RS + RS

QR  =  4RS

RS  =  QR/4

By applying Pythagorean theorem in a triangle PQS, we get

PQ²  =  PS² + QS²

PS²  =  PQ² - QS²  -----(1)

By applying Pythagorean theorem in a triangle PRS, we get

PR²  =  PS² + SR²

PS²  =  PR² - SR² -----(2)

PQ² - QS²   =  PR² - SR²

PQ² - QS²   =  PR² - SR²

PQ²   =  PR² - SR²   + QS² 

PQ²   =  PR² - SR²   + (QR - RS)² 

PQ²   =  PR² - SR²  + QR² + RS² - 2QR x RS

PQ²   =  PR² + QR² - 2QR x RS

PQ²   =  PR² + QR² - 2 QR x (QR/4)

PQ²   =  PR² + QR² - (QR²/2)

PQ²   =  (2PR² + 2QR² - QR²)/2

2PQ²   =  2PR² + QR²

Problem 3 :

In the adjacent figure, ABC is a right angled triangle with right angle at B and points D, E trisect BC. Prove that 8AE² = 3AC² + 5AD²

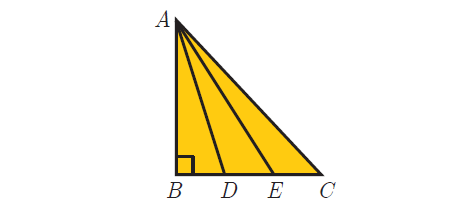
Solution :

AE² = AB² + (2x)²

AE² = AB² + 4x²

In Δ ABC,

AC² = AB² + BC²  

AC² = AB + (3x)² 

AC² = AB² + 9x²

Now,

3AC² + 5AD² = 3(AB² + 9x²) + 5(AB² + x²) 

=  8AB² + 32x²

=  8(AB² + 4x²)

= 8AE²

8AE² = 3AC² + 5AD²

Hence proved.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.