PRACTICE MATH PROBLEMS FOR 7TH GRADERS

Question 1 :

What is the square root of 196?

(A) 14                (B) 19                 (C) 12

Solution :

To find the square root of 196, we have to decompose 196 into prime factors.

√196  =  √(2 ⋅ 7 ⋅ 2 ⋅ 7)

=  2 ⋅ 7

=  14

Hence the square root of 196 is 14.

Question 2 :

A play ground is 100 m long and 70 m wide. How much distance does a girl run when she runs 5 times around the playground?

(A) 2500 m      (B) 2300 m        (C) 1700 m

Solution :

Distance covered by the girl

=  5 (perimeter of the ground) 

Ground is in the shape of rectangle

Perimeter of rectangle  =  2(length + width)

  =  2(100 + 70)

  =  2(170)  =  340

5 (perimeter of the ground)  =  5(340)  =  1700 m

Hence the required distance covered by the girl is 1700 m.

Question 3 :

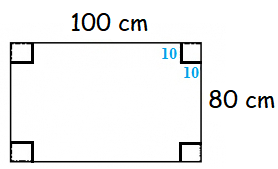
From a rectangular sheet of tin, of size 100 cm by 80 cm, are cut four squares of side 10 cm from each corner. Find the area of the remaining sheet.

(A) 2400 cm²      (B) 3600 cm²        (C) 7600 cm²

Solution :

Length of the rectangular sheet  =  100 cm

Breadth of the rectangular sheet  =  80 cm

Area of the rectangular sheet of tin

=  100 cm ⋅ 80 cm

=  8000 cm²

Side of the square at the corner of the sheet  =  10 cm

Area of one square at the corner of the sheet

=  (10 cm)² 

=  100 cm²

Area of 4 squares at the corner of the sheet

=  4 ⋅ 100

=  400 cm²

Hence, Area of the remaining sheet of tin

=  Area of the rectangular sheet - Area of the 4 squares

Area of the remaining sheet of tin

=  (8000 - 400)

=  7600 cm²

Question 4 :

If x = 2, y = 3 and z =-2 then find the value of 6x-7y + 4z

(A) 12                  (B) -17             (C) -10

Solution :

Applying the values of the variables in the given expression, we get

 6x-7y + 4z  =   6 (2) - 7 (3) + 4 (-2)

  =  12 - 21 - 8

  =  12 - 39

  =  -27

Hence the answer is -27.

Question 5 :

Find the value of x in 4^4x-7 = 4 ^x-1

(A) 2            (B) 5            (C) 3

Solution :

4^4x-7 = 4 ^x-1

Since the bases are equal, we may equate the powers

4x - 7  =  x - 1

Subtract x from both sides

4x - x - 7 =  -1 

Add both sides by 7

3x  =  -1 + 7

3x  =  6

Divide both sides by 3

x  =  6/3  =  2

Hence the answer is is 2.

Question 6 :

Expand (x  + 5y)²

(A) x² + 10 xy + 25y²      (B) x² - 10 xy - 25y²   

(C) x² + 10 xy - 25y²

Solution :

(x  + 5y)²

To find the expansion of the above algebraic expression, we need to use the algebraic identity.

(x  + 5y)²  =  a² + 2ab + b²

a = x, b = 5y

  =  x² + 2x(5y) + (5y)²

  =  x² + 10x + 5²y²

  =  x² + 10x + 25y²

So, the answer is x² + 10x + 25y².

Question 7 :

On selling a clock for $240, a trader loses 4%. In order to gain 10%, he must sell the clock for

(A) $275      (B) $295      (C) $365

Solution :

Given S.P  =  $240  and Loss  =  4 %

96% of C.P  =  $240

C.P  =  (240 x 100)/96  =  $250

10% profit on C.P = $25

So, S.P. with 10 % profit = 250 + 25 = $275

Question 8 :

Find the remainder when 8x³ - 12 x² + 6x +15 divided by 2x-3. 

(A) 20         (B) 24         (C) 10

Solution :

Let us use the concept Remainder theorem

f(x)  =  8x³ - 12 x² + 6x +15

2x - 3  =  0 ==>  x  =  3/2

f(3/2)  =  8(3/2)³ - 12(3/2)² + 6(3/2) + 15

=  8 (27/8) - 12(9/4) + 9 + 15

=  27 - 3(9) + 9 + 15

=  27 - 27 + 9 + 15

=  24

So, the remainder is 24.

Question 9 :

The difference of two numbers is 72 and quotient obtained by dividing the one by other is 3. Find the numbers.

(A) 25, 97             (B) 15, 87          (C) 36, 108

Solution :

Let "x", "y" be the required numbers

x - y  =  72  ----(1)

x / y  = 3  ----(2)

x  =  3y

Applying the value of x in the first equation, we get

3y - y = 72

2y  =  72  ==> y  =  36

x  =  3(36)  =  108

Hence the required numbers are 36 and 108.

Question 10 :

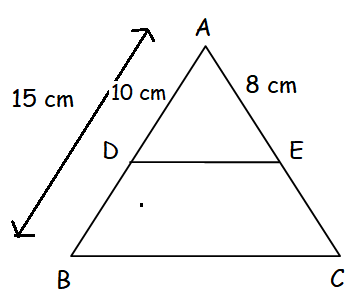
In triangle ABC, DE parallel to EC find AC when AB = 15 cm, AD = 10 cm and AE = 8 cm 

(A) 8 cm      (B) 4 cm      (C) 2 cm

Solution :

So, the answer is 4 cm.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.