PRACTICE PROBLEMS BASED ON BPT THEOREM

Question 1 :

In fig. if PQ || BC and PR || CD prove that

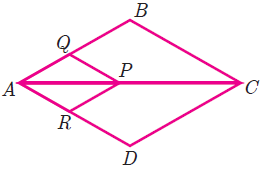
(i)  AR/RD  =  AQ/AB

Solution :

PQ || BC

AP/PC  =  AQ/QB   ---(1)

PR || CD

AP/PC  =  AR/RD   ---(2)

(1)  =  (2)

AQ/QB  =  AR/RD

(ii)  QB/AQ  =  DR/AR

Solution :

Taking reciprocal on the first result, we get

QB/AQ  =  DR/AR

Question 2 :

Rhombus PQRB is inscribed in ΔABC such that ÐB is one of its angle. P, Q and R lie on AB, AC and BC respectively. If AB = 12 cm and BC = 6 cm, find the sides PQ, RB of the rhombus

Solution : 

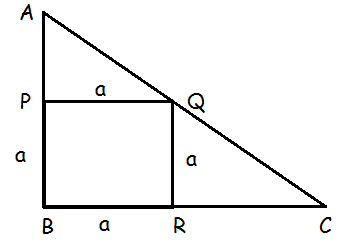
In triangle ABC, BC is parallel to PQ.

Let side of rhombus be a cm.

Given AB = 12 cm. So AP = 12 – a

BC = 6 cm

We have AP / AB = PQ / BC

12 – a / 12 = a / 6

12 a = 72 – 6 a

18 a = 72

a = 72 / 18

a = 4 cm

PQ  =  4 cm and RB  =  4 cm

Question 3 : 

In trapezium ABCD, AB || DC , E and F are points on non-parallel sides AD and BC respectively, such that EF || AB . Show that AE/ED  =  BF/FC

Solution :

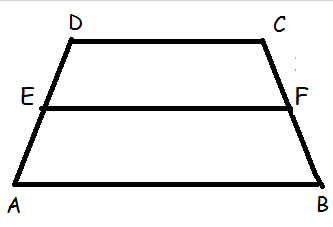
Let us join the vertices D and B which intersects the side EF at the point T.

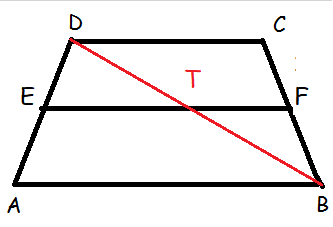
In triangle DAB,

DE/EA  =  DT/TB -----(1)

In triangle DBC

BT/TD  =   BF/FC -----(2)

Now let us take the reciprocal of (2) and equate them with (1). So we get 

TD/BT  =  FC/BF

DE/DA  =  FC/BF

Take reciprocal on both sides, we get

DA/DE  =  BF/FC

Hence proved.

Question 4 :

In figure DE || BC and CD || EF. Prove that AD² = AB×AF

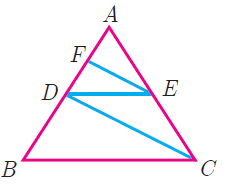
Solution :

In triangle ABC,

AD/DB  =  AE/EC ------(1)

In triangle ADC,

AF/FD  =  AE/EC -----(2)

(1)  =  (2)

AD/DB  =  AF/FD

Taking reciprocal on both side, so we get 

DB/AD  =  FD/AF

Add 1 on both sides, we get

(DB/AD) + 1  =  (FD/AF ) + 1

(DB + AD)/AD  =  (FD + AF)/AF

AB/AD  =   AD/AF

AD²  =  AB x AF

Hence proved.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.