PRACTICE PROBLEMS ON CYCLIC QUADRILATERAL

Question 1 :

Find the value of x in the given figure. 

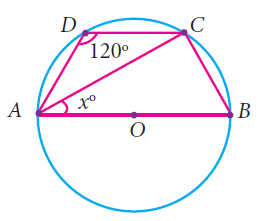
Solution :

In triangle ACB,

<ACB  =  90 (Angle in a semicircle)

Sum of opposite angles in a quadrilateral  =  180

<ADC + <ABC  =  180

120 + <ABC  =  180

<ABC  =  60

<ACB + <CAB + <ABC  =  180

x + 90 + 60  =  180

x + 150  =  180

x  =  180 - 150

x  =  30

Question 2 :

In the given figure, AC is the diameter of the circle with centre O. If <ADE = 30° ; <DAC = 35° and <CAB = 40°. Find (i) <ACD   (ii)  <ACB  (iii)  <DAE

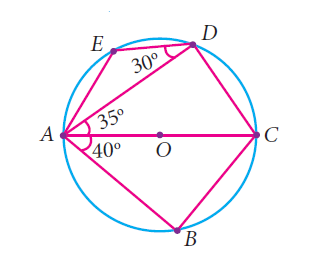
Solution :

In triangle ADC,

<ADC  =  90 (angle in a semicircle)

<ADC + <DAC + <ACD  =  180

90 + 35 + <ACD  =  180

<ACD  =  180 - 125

<ACD  =  55

In triangle ACB,

<ACB + <ABC + <BAC  =  180

<ACB + 90 + 40  =  180

<ACB  =  180 - 130

<ACB  =  50

(iii)  <EDA + <ADC  + <EAD + <DAC  =  180

(Sum of opposite angles in a quadrilateral)

30 + 90 + <EAD + 35  =  180

<EDA  =  180 - 155

<EDA  =  25

Question 3 :

Find all the angles of the given cyclic quadrilateral ABCD in the figure.

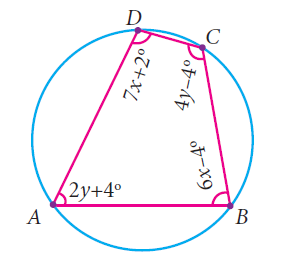
Solution :

<A + <C  =  180

2y + 4 + 4y - 4  =  180

6y  =  180

y  =  180/6

y  =  30

<B + <D  =  180

6x - 4 + 7x + 2  =  180

13x - 2  =  180

13x  =  182

x  =  182/13

x  =  14

<A  =  2y + 4  =  2(30) + 4  =  60 + 4  =  64

<B  =  6x - 4  =  6(14) - 4  =  84 - 4  =  80

<C  =  4y - 4  =  4(30) - 4 =  120 - 4  =  116

<D  =  7x + 2  =  7(14) + 2  =  100

Question 4 :

In the given figure, ABCD is a cyclic quadrilateral where diagonals intersect at P such that <DBC = 40° and <BAC = 60° find

(i)  <CAD   (ii)  BCD

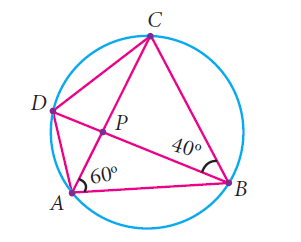
Solution :

Angles in a same segment will be equal.

<DAC  =  <DBC  =  40

In ΔBCD, we have:

∠BCD + ∠DBC + ∠BDC = 180° 

(Angle sum property of a triangle)

<BCD + 60° + 40° = 180°

∠BCD = (180° - 100°) = 80°

Question 5 :

Find the value of x if ABCD is a cyclic quadrilateral if ∠1 : ∠2 = 3 : 6.

a) 90°         b) 45°       c) 60°     d) 20°

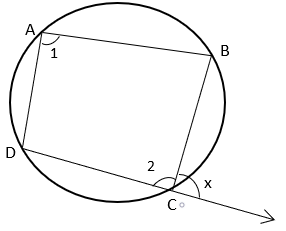
Solution :

In cyclic quadrilateral, the sum of opposite angles is equal to 180 degree.

The ratio between ∠1 and ∠2  is = 3 : 6

Let ∠1 = 3a and ∠2 = 6a

∠1 + ∠2 = 3a + 6a

9a = 180

a = 180/9

a = 20

By observing the figure above, 

∠2 + x = 180

 ∠2 = 6(20) ==> 120

120 + x = 180

x = 180 - 120

x = 60

Question 6 :

ABCD is a cyclic parallelogram. Show that it is a rectangle.

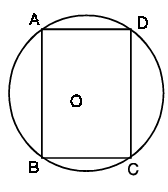
Solution :

In any cyclic quadrilateral, sum of opposite angles is equal to 180 degree.

∠B + ∠D = 180

In a parallelogram, the opposite angles are equal.

∠B = ∠D

∠B + ∠B = 180

2∠B = 180

∠B = 90 degree

So, the ABCD is a rectangle.

Question 7 :

If PQRS is a cyclic quadrilateral and PQ is diameter, find the value of ∠PQS.

a) 45°    b) 110°    c) 20°     d) 80°

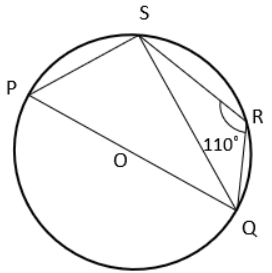
Solution :

∠SRQ + ∠SPQ = 180

110 + ∠SPQ = 180

∠SPQ = 180 - 110

∠SPQ = 70

∠PSQ = 90 (angle in a semicircle)

In triangle PSQ, 

∠PSQ + ∠SPQ + ∠PQS = 180

90 + 70 + ∠PQS = 180

160 +  ∠PQS = 180

∠PQS = 180 - 160

∠PQS = 20

Question 8 :

Find the value of x and y if ABCD is cyclic quadrilateral.

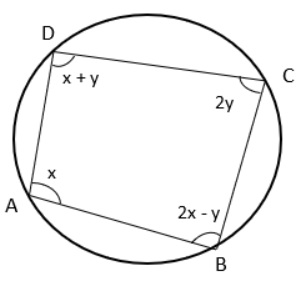
a) 60°, 60°    b) 50°, 60°    c) 45°, 45°    d) 80°, 90

Solution :

∠A + ∠C = 180

x + 2y = 180  -------(1)

∠B + ∠D = 180

x + y + 2x - y = 180 

3x = 180

x = 180 / 3

x = 60

Applying the value of x, we get

60 + 2y = 180

2y = 180 - 60

2y = 120

y = 120 / 2

y = 60

So, option a is correct.

Question 9 :

What is the value of ∠PQR if PQRS is cyclic quadrilateral and PS = SR?

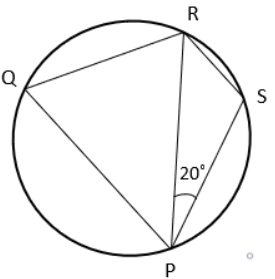
a) 90°     b) 70°    c) 40°    d) 30°

Solution :

In a triangle PSR,

∠PSR + ∠SPR + ∠SRP = 180

∠PSR + 20 + 20 = 180

∠PSR + 40 = 180

∠PSR = 180 - 40

∠PSR = 140

∠RQP + ∠PSR = 180

∠RQP + 140 = 180

∠RQP = 180 - 140

∠RQP = 40

So, option c is correct.

Question 10 :

What is the value of ∠PRQ if ∠PSR : ∠PQR = 1 : 2?

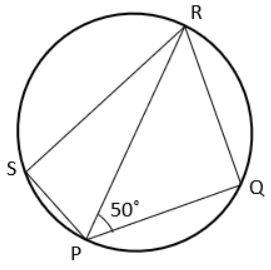
a) 50°     b) 10°    c) 90°     d) 45°

Solution :

Given that, ∠PSR : ∠PQR = 1 : 2

∠PSR = x and ∠PQR = 2x

x + 2x = 180

3x = 180

x = 180/3

x = 60

In triangle PRQ,

∠PQR + ∠QRP + ∠RPQ = 180

∠PQR = 2x

= 2(60)

∠PQR = 120

120 + ∠QRP + 50 = 180

170 + ∠QRP = 180

∠QRP = 180 - 170

∠QRP = 10

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.