PRACTICE PROBLEMS ON FINDING CENTRIOD OF A TRIANGLE WITH COORDINATES

Definition of centroid :

Consider a triangle ABC whose vertices are A(x₁, y₁), B(x₂ , y₂ ) and C(x₃ , y₃). Let AD, BE and CF be the medians of the triangle ABC.

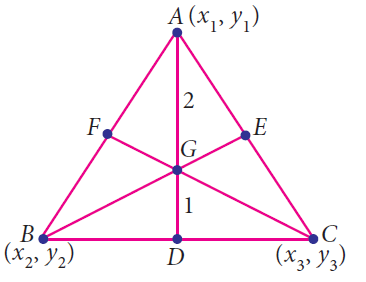
The centroid G of the triangle with vertices A(x₁, y₁), B(x₂ , y₂ ) and C(x₃ , y₃) is

  =  [ (x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3 ]

In the above triangle , AD, BE and CF are called medians. All the three medians AD, BE and CF are intersecting at G. So  G is called centroid of the triangle 

Question 1 :

Find the centroid of triangle whose vertices are (1, 10) (-7, 2) and (-3, 7).

Solution :

Let the vertices be A (1, 10) B (-7, 2) and  C (-3, 7)

x₁  =  1, x₂  =  -7, x₃  =  -3

y₁  =  10, y₂  =  2, y₃  =  7 

Centroid of a triangle  =  (x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3

  =  [ 1+(-7)+(-3)/3 , (10+2+7) ]/ 3

  =  (1-7-3)/3, 19/3

  =  (-9/3 , 19/3)

  =  (-3, 19/3)

Question 2 :

Find the centroid of triangle whose vertices are (-1, -3) (2, 1) and (2, -4).

Solution :

Let the vertices be A (-1, -3) B (2, 1) and C (2, -4).

x₁  =  -1, x₂  =  2, x₃  =  2

y₁  =  -3, y₂ = 1, y₃  =  -4 

Centroid of a triangle  =  (x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3

  =  [ ((-1)+2+2)/3, ((-3)+1+(-4))/3]

  =  [ (-1 + 4)/3, (-3+1-4)/3 ] 

  =  [3/3, (-7 + 1)/3   

  =  [ 1, (-6/3) ]

  =  (1, -2)

Question 3 :

Find the centroid of triangle whose vertices are (1, 1) (2, 3) and (-2, 2).

Solution :

Let the vertices be A (1, 1) B (2, 3) and  C (-2, 2)

x₁  =  1, x₂  =  2, x₃  =  -2

y₁  =  1, y₂  =  3, y₃  =  2 

Centroid of a triangle  =  (x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3

  =  [(1+2+(-2))/3, (1+3+2)/3]

  =  [ (3 - 2)/3 , (6/3) ]

  =  (1/3 , 2)

Question 4 :

Find the centroid of triangle whose vertices are (1, 3) (2, 7) and (5, 4).

Solution :

Let the vertices be A (1, 3) B (2, 7) and  C (5, 4)

x₁  =  1, x₂  =  2, x₃  =  5

y₁  =  3, y₂  =  7, y₃  =  4 

Centroid of a triangle  =  (x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3

  =  [ (1+2+5)/3, (3+7+4)/3 ]

  =  [ (3+5)/3, (10+4)/3 ]

  =  (8/3, 14/3)

Question 5 :

Find the centroid of triangle whose vertices are (6, 7) (2, -9) and (-4, 1).

Solution :

Let the vertices be A (6, 7) B (2, -9) and  C (-4, 1)

x₁  =  6, x₂ = 2, x₃  =  -4

y1  =  7, y₂  =  -9, y₃  =  1 

Centroid of a triangle   =  (x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3

  =  [ (6+2+(-4))/3 , (7+(-9)+1)/3

  =  (8 - 4)/3 , (8 - 9)/3 

  =  (4/3 , -1/3)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.