PRACTICE PROBLEMS ON FINDING THE AREA OF TRAPEZIUM
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
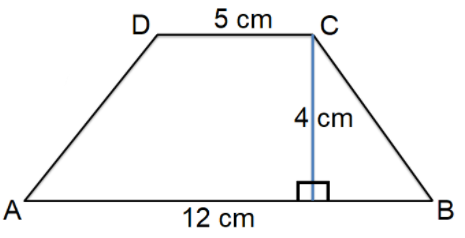
Problem 2 :
The shape of the top surface of a table is a trapezium. Find its area, if its parallel sides are 1 m and 1.2 m and perpendicular distance between 0.8 m.
Problem 3 :
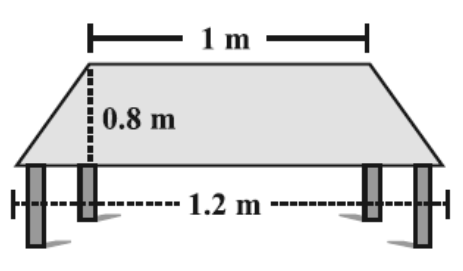
The wall is in the shape as shown below has to be painted. If one can of paint covers 0.5 m2, how many cans of paint will be needed, if only one coat of paint is applied ?
Problem 4 :
The two parallel sides of a trapezium are 1.5 m and 2.5 m respectively. If the perpendicular distance between them is 6.5 meters, the area of the trapezium is :
a) 10 m2 b) 13 m2 c) 20 m2 d) 26 m2
Problem 5 :
The area of the field in the shape of trapezium measures 1440 m2. The perpendicular distance between its parallel sides is 24 m. If the ratio of the parallel sides is 5 : 3 the length of the longer parallel side is :
a) 45 m b) 60 m c) 75 m d) 120 m
Problem 6 :
The cross section of a canal is trapezium in shape. The canal is 12 m wide at the top and 8 m wide at the bottom. If the area of the cross The area of the cross section is 840 sq.cm the depth of the canal is :
a) 8.75 m b) 42 m c) 63 m d) 84 m
Answer Key
1) 34 cm2
2) the lengths of the two parallel sides are 15 cm and 17 cm.
3) 8.8 m2
4) 85 cans of paint required to cover the above wall.
5) 13 m2
6) the length of longer parallel side is 75 m.
7) h = 84 cm
Problem 1 :
A section of a deck is in the shape of a trapezoid. What is the area of this section of the
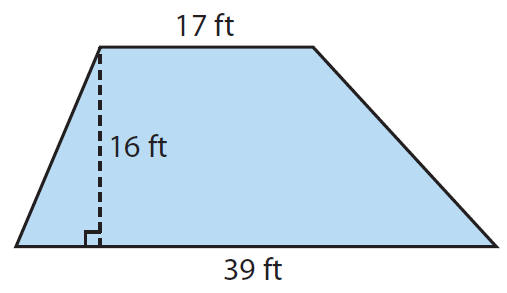
Problem 2 :
The length of one base of a trapezoid is 27 feet, and the length of the other base is 34 feet. The height is 12 feet. What is its area?
Problem 3 :
Simon says that to find the area of a trapezoid, you can multiply the height by the top base and the height by the bottom base. Then add the two products together and divide the sum by 2. Is Simon correct? Explain your answer
Problem 4 :
The height of a trapezoid is 8 in. and its area is 96 square inches. One base of the trapezoid is 6 inches longer than the other base. What are the lengths of the bases?
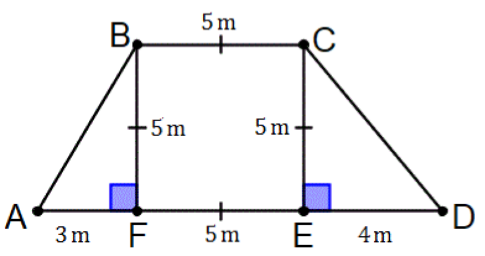
Problem 5 :
Mr Taylor keeps chickens in the field shown. Each chicken needs 3m². What is the maximum number of chickens he can keep in the field?
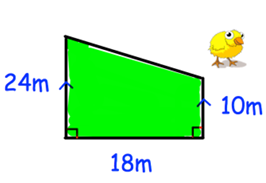
Problem 6 :
The trapezium and the triangle have the same area. Calculate the height of the triangle.
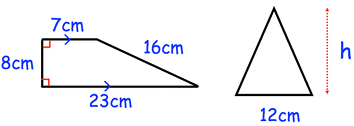
Problem 7 :
Shown is a rectangular garden. There is a flowerbed in the shape of a trapezium. What percentage of the garden does the flowerbed cover?
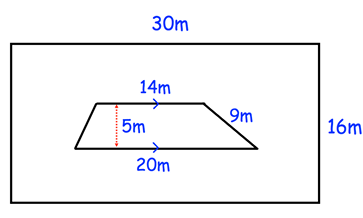
Problem 8 :
Farmer Richards owns this field. The crop he plants earns him £7 for each square metre How much money does he earn in total?
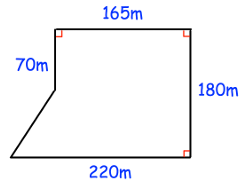
Problem 9 :
A badge is made by joining two congruent trapezia. Find the area of the badge.
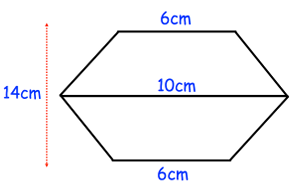
Problem 10 :
A shape has been made from joining a rectangle, trapezium and triangle. The height of the shape is 3.5cm. The ratio of the height of the rectangle to the height of the trapezium to the height of the triangle is 2:3:2. Calculate the area of the
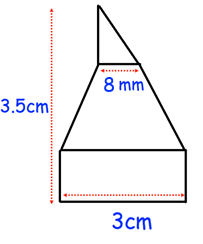
Answer Key
1) 448 ft2
2) 366 ft2
3) Yes
4) the lengths of the bases are 15 inches and cm and 9 inches.
5) 102 chickens
6) height of the triangle is 20 cm.
7) 564%.
8) 32725 m2
9) 112 m2
10) 36.25 cm2
Word Problems on Finding Area of Trapezium
Problem 1 :
In a trapezium the measurement of one parallel side two more than the other parallel side and the height is 4 cm. The area of the trapezium is 64 cm2. Find the lengths of the two parallel sides.
Problem 2 :
Find the area of a trapezium whose parallel sides are 24 cm and 20 cm and the distance between them is 15 cm.
Problem 3 :
The area of a trapezium is 1586 sq. cm. The distance between its parallel sides is 26 cm. If one of the parallel sides is 84 cm then, find the other side.
Problem 4 :
The area of a trapezium is 1080 sq. cm. If the lengths of its parallel sides are 55.6 cm and 34.4 cm, find the distance between them.
Problem 5 :
The area of a trapezium is 180 sq. cm. and its height is 9 cm. If one of the parallel sides is longer than the other by 6 cm, find the length of the parallel sides.
Problem 6 :
The sunshade of a window is in the form of isosceles trapezium whose parallel sides are 81 cm and 64 cm and the distance between them is 6 cm. Find the cost of painting the surface at the rate of $ 2 per sq. cm.
Problem 7 :
A window is in the form of trapezium whose parallel sides are 105 cm and 50 cm respectively and the distance between the parallel sides is 60 cm. Find the cost of the glass used to cover the window at the rate of $ 15 per 100 sq. cm.
Problem 8 :
The length of one base of a trapezoid is 27 feet, and the length of the other base is 34 feet. The height is 12 feet. What is its area?
Problem 9 :
The height of a trapezoid is 8 in. and its area is 96 square inches. One base of the trapezoid is 6 inches longer than the other base. What are the lengths of the bases?
Answers :
1) a = 17 cm and b = 15 cm
2) A = 330 sq. cm
3) Length of the other side is 38 cm
4) h = 24 cm
5) a = 17 cm and b = 23 cm
6) $ 870
7) $ 697.5
8) A = 366 ft2
9) Lengths of the bases are 15 inches and cm and 9 inches.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
GMAT Quantitative Reasoning Questions and Answers
Dec 27, 25 09:33 PM
GMAT Quantitative Reasoning Questions and Answers -
10 Hard SAT Math Questions (Part - 40)
Dec 25, 25 08:30 AM
10 Hard SAT Math Questions (Part - 40) -
10 Hard SAT Math Questions (Part - 41)
Dec 24, 25 07:58 PM
10 Hard SAT Math Questions (Part - 41)

