PRACTICE PROBLEMS ON INVERSE OF SINE FUNCTIONS
Question 1 :
Find all the values of x such that
(i) −10π ≤ x ≤10π and sin x = 0
Solution :
sin x = 0
x = sin-1 (0)
Now we have to find the angles of sin for which we will get the value 0.
The value of sin π = 0, the value of sin 2π = 0. For all odd and even π's, we will get 0.
By generalizing this, we get
x = nπ, n = 0, ±1, ±2,.........
(ii) −8π ≤ x ≤ 8π and sin x = −1.
Solution :
sin x = -1
x = sin-1 (-1)
Now we have to find the angles of sin for which we will get the value -1.
The value of sin 3π/2 = -1, the value of sin [(3π/2) + π] = -1.
By generalizing this, we get
x = (4n - 1)π/2, n = 0, ±1, ±2,.........
Finding Period and Amplitude of Sin Functions
The amplitude is the maximum distance of the graph from the x -axis. Thus, the amplitude of a function is the height from the x -axis to its maximum or minimum. The period is the distance required for the function to complete one full cycle.
(i) The graph of a periodic function consists of repetitions of the portion of the graph on an interval of length of its period.
(ii) The graph of an odd function is symmetric with respect to the origin and the graph of an even function is symmetric about the y -axis.
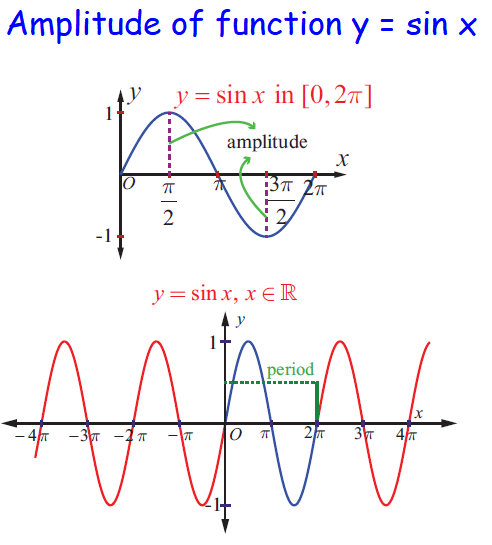
How to find amplitude and period of sin function ?
y = A sin Bx, y = A cos Bx, y = A tan Bx
- amplitude = |A|
- period = 2π/B
By comparing the given trigonometric function with general form, we get amplitude and period.
Question 2 :
Find the period and amplitude of
(i) y = sin 7x
Solution :
A = 1 and B = 7
Amplitude = |1| = 1
Period = 2π/B = 2π/7
(ii) y = - sin (1/3)x
Solution :
A = -1 and B = 1/3
Amplitude = |-1| = 1
Period = 2π/B = 2π/(1/3)
Period = 6 π
(iii) y = 4 sin (-2x)
Solution :
y = - 4 sin (2x)
A = -4 and B = 2
Amplitude = |-4| = 4
Period = 2π/B = 2π/2
Period = π
Question 3 :
Sketch the graph of y = sin (1/3)x for 0 ≤ x ≤ 6π
Solution :
y = sin (1/3)x
A = 1 and B = 1/3
Amplitude = |1| = 1
Period = 2π/B = 2π/(1/3)
Period = 6π
In order to graph the given function, let us consider the graph of y = sin x.
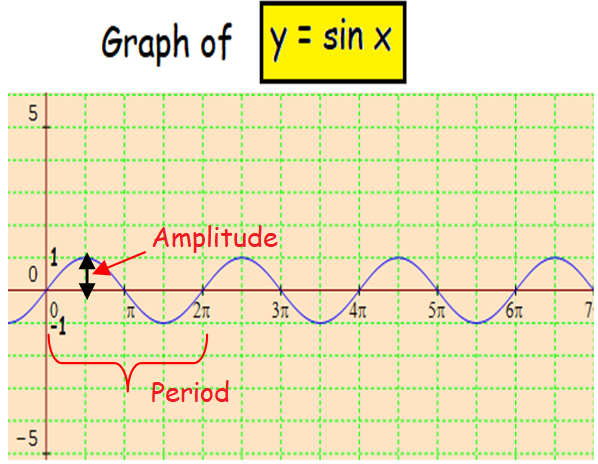
From the above graph, we have to repeat the same amplitude and extend the period of the curve upto 6π
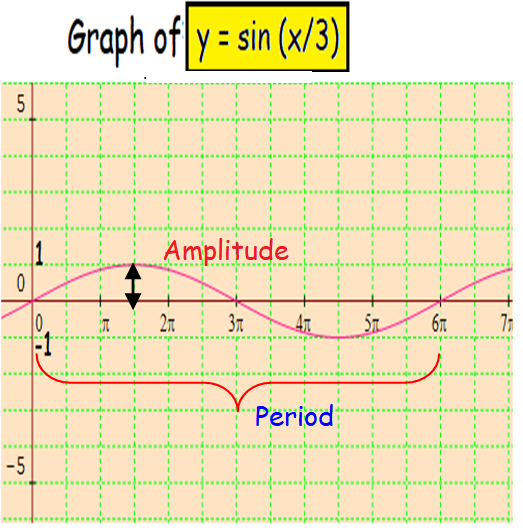
Question 4 :
Find the value of
(i) sin-1 (sin (2π/3))
Solution :
y = sin-1 (sin (2π/3))
The value of 2π/3 is 120. It lies in second quadrant. Now we have to represent this 120 degree using ASTC formula.
So, we get
y = sin-1 (sin (π - (π/3)))
y = π/3
(ii) sin-1 (sin (5π/4))
Solution :
y = sin-1 (sin (5π/4))
The value of 5π/4 is 225. It lies in third quadrant. Now we have to represent this 225 degree using ASTC formula.
So, we get
y = sin-1 (sin (π + (π/4)))
For third quadrant, we have negative sign for sin.
y = -π/4
Question 5 :
For what value of x does sin x = sin−1 x ?
Solution :
For angle "0" for sin, we get the value sin x as 0.
From the value sin−1 0, we get the value 0.
Question 6 :
Find the domain of the following
(i) f(x) = sin-1 [(x2 + 1)/2x)]
Solution :
f(x) = sin-1 [(x2 + 1)/2x)]
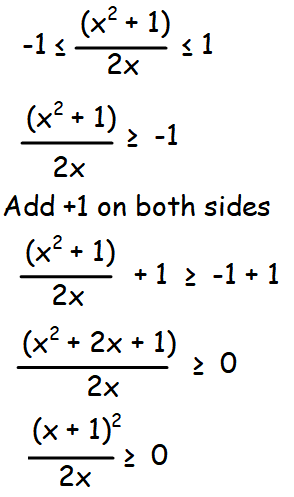
In order to make the statement given above true, we have to apply the values of x greater than 0.
x ∈ (0, ∞) U {-1} ----(1)
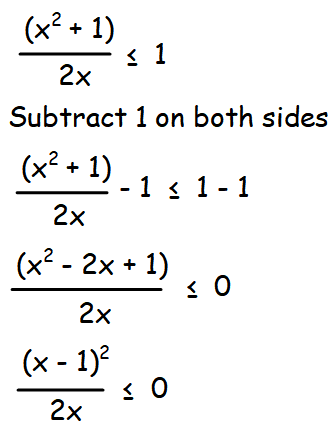
In order to make the statement given above true, we have to apply the values of x lesser than than 0.
x ∈ (-∞, 0) U {1} ----(2)
Now we have to find the intersection of (1) and (2).
-1 lies in (-∞, 0) and 1 lies in (0, ∞). Hence the required domain is {-1, 1}.
(ii) g(x) = 2sin−1 (2x −1) − (π/2)
Solution :
-1 ≤ 2x - 1 ≤ 1
Add 1 through out the inequality
-1 + 1 ≤ 2x - 1 + 1 ≤ 1 + 1
0 ≤ 2x ≤ 2
Divide through out the inequality by 2
0 ≤ x ≤ 1
Hence the required domain is [0, 1].
Question 7 :
Find the value of sin-1(sin 5π/9 cos π/9 + cos 5π/9 sin π/9)
Solution :
= sin-1(sin 5π/9 cos π/9 + cos 5π/9 sin π/9)
= sin-1[sin (5π/9 + π/9)]
= sin-1[sin (6π/9)]
= 6π/9
= 2π/3
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 150)
Apr 25, 25 11:46 AM
Digital SAT Math Problems and Solutions (Part - 150) -
AP Calculus AB Problems with Solutions (Part - 19)
Apr 24, 25 11:10 PM
AP Calculus AB Problems with Solutions (Part - 19) -
AP Calculus AB Problems with Solutions (Part - 18)
Apr 24, 25 11:06 PM
AP Calculus AB Problems with Solutions (Part - 18)
