PRACTICE PROBLEMS ON MATRICES FOR GRADE 10
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Question 1 :
If –4 is a root of the equation x2 + px −4 = 0 and if the equation x2 + px +q = 0 has equal roots, find the values of p and q.
Solution :
Let p(x) = x2 + px −4
Since -4 is one of the root of the quadratic equation
p(-4) = (-4)2 + p(-4) −4
0 = 16 - 4p - 4
12 - 4p = 0
4p = 12
p = 3
By applying the value in the first equation, we get
x2 + px −4 = 0
x2 + 3x −4 = 0
(x - 1)(x + 4) = 0
x = 1 and x = -4.
By applying the value of p in the second equation, we get
x2 + 3x + q = 0
Since the above quadratic equation will have equal roots,
b2 - 4ac = 0
32 - 4(1)q = 0
-4q = -9
q = 9/4
Question 2 :
Two farmers Senthil and Ravi cultivates three varieties of grains namely rice, wheat and ragi. If the sale (in ₹) of three varieties of grains by both the farmers in the month of April is given by the matrix.
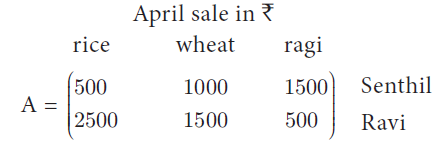
and the May month sale (in ₹) is exactly twice as that of the April month sale for each variety.
(i) What is the average sales of the months April and May.
(ii) If the sales continues to increase in the same way in the successive months, what will be sales in the month of August?
Solution :
In order to find the sales on May month, we multiply the April month sales by 2.
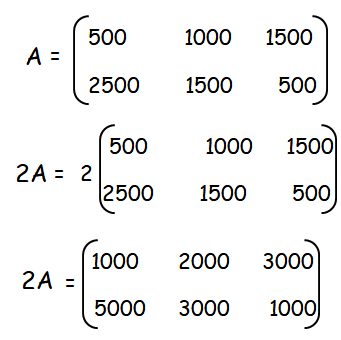
(i) What is the average sales of the months April and May
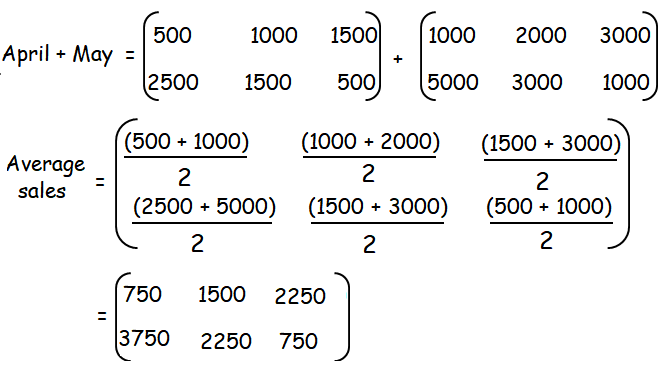
(ii)

Question 3 :
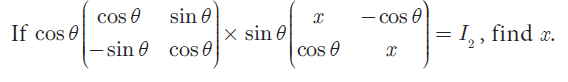
Question 4 :
Given
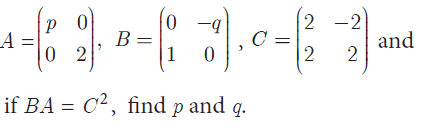
Solution :
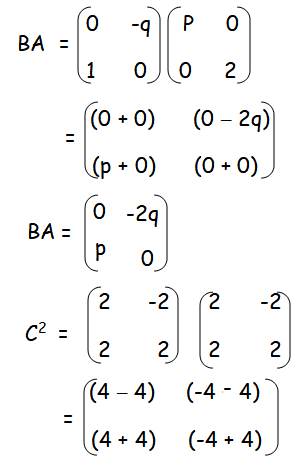
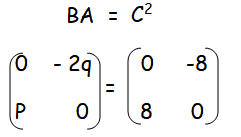
By equating the corresponding terms, we get
-2q = -8
q = 4
p = 8
Hence the values of p and q are 8 and 4 respectively.
Question 5 :
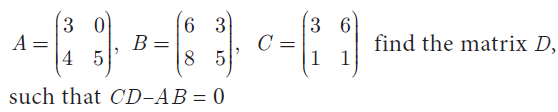
Solution :
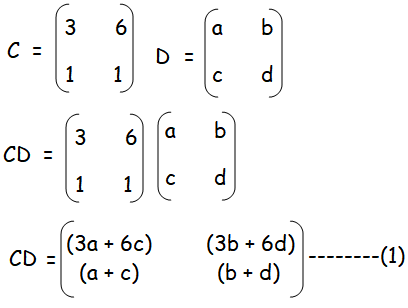
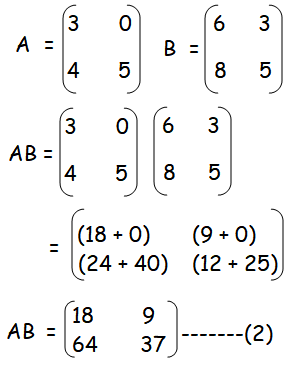
Equating the corresponding terms, we get
CD - AB = 0
3a + 6c - 18 = 0
3a + 6c = 18
a + 2c = 6 ------(3)
a + c - 64 = 0
a + c = 64------(4)
(3) - (4)
c = 6 - 64
c = -58
By applying the value of c in (3), we get
a + 2(-58) = 6
a - 116 = 6
a = 6 + 116
a = 122
3b + 6d = 9
b + 2d = 3 -----(5)
b + d = 37 -----(6)
(5) - (6)
2d - d = 3 - 37
d = -34
By applying the value of d in (5), we get
b + 2(-34) = 3
b - 68 = 3
b = 3 + 68
b = 71
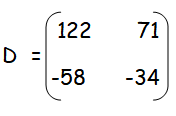
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
SAT Math Problems and Solutions
Feb 14, 26 06:05 AM
SAT Math Problems and Solutions -
SAT Math Practice Questions with Answers
Feb 14, 26 05:47 AM
SAT Math Practice Questions with Answers -
SAT Math Practice Test with Answers
Feb 14, 26 02:30 AM
SAT Math Practice Test with Answers

