PRACTICE PROBLEMS ON RATIONALIZING DENOMINATOR

Question 1 :

Rationalize the denominator

(i)  1/√50

Solution :

In order to rationalize the denominator, we have to multiply both numerator and denominator of the given rational number by √50.

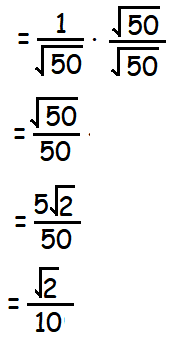
(ii)  5/3√5

Solution :

  =  5/3√5

Let us multiply the numerator and denominator by √5.

  =  (5/3√5) ⋅ (√5/√5)

 =  5√5/3(5)

  =   √5/3

Hence the answer is √5/3.

(iii)  √75/√18

Solution :

  =  √75/√18

  = 5 √3/3√2

  =  (5/3) (√3/√2)

Multiply both numerator and denominator by √2, we get

  =  5 √6/6

Hence the answer is 5 √6/6.

(iv)  3√5/√6

Solution :

  =  3√5/√6

  = (3√5/√6) ⋅ (√6/√6)

=  3√30/6

=  √30/2

Hence the answer is √30/2.

Question 2 :

Rationalize the denominator and simplify

(i)  (√48 + √32) / (√27 - √18)

Solution :

Since the denominator is of 2 terms, we have to multiply the numerator and denominator by the conjugate of denominator.

  =  [(√48 + √32) / (√27 - √18)] ⋅ [(√27+√18)/(√27+√18)]

  =  (√48 + √32)(√27+√18) / (27 - 18)

  =  (√(48 ⋅ 27) + √(48 ⋅ 18) + √(32 ⋅ 27) + √(32 ⋅ 18)/9

  =  (36 + 12√6 + 12√6 + 24)/9

  =  (60 + 24√6)/9

  =  (20 + 8√6)/3

  =  (4/3)(5 + 2√6)

(ii)  (5√3 + √2) / (√3 + √2)

Solution :

  =  (5√3 + √2) / (√3 + √2)

  =  [(5√3 + √2) / (√3 + √2)] ⋅ [(√3 - √2) / (√3 - √2)]

  =  (5(3) - 5√6 + √6 - 2) / (3 - 2)

  =  (15 - 6√6 - 2) / 1

  =  13 - 6√6

(iii)  (2√6 - √5) / (3√5 - 2√6)

Solution :

=  (2√6 - √5) / (3√5 - 2√6)

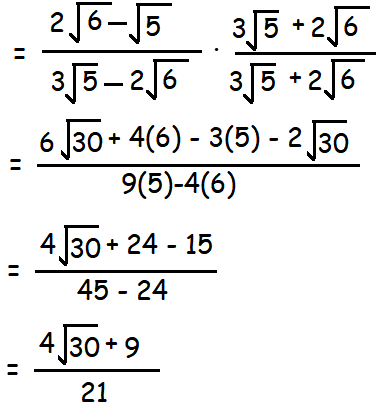
(iv)  [√5/(√6 + 2)] - [√5/(√6 - 2)]

Solution :

   =   [√5/(√6 + 2)] - [√5/(√6 - 2)]

  =  [√5(√6 - 2) - √5(√6 + 2)]/(√6 - 2)(√6 + 2)

  =  [√30 - 2√5 - √30 - 2√5)]/(6 - 4)

  =  -4√5/2

  =  -2√5

Question 3 :

Find the value of a and b if

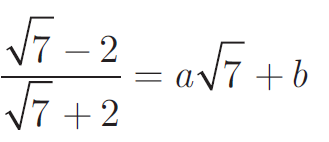
Solution :

  =  [(√7 - 2)/(√7 + 2)] ⋅ [(√7 - 2)/(√7 - 2)]

  =  [(√7 - 2)²/(√7 + 2)(√7 - 2)]

  =  (7 - 4√7 + 4)/(7 - 4)

  =  (11 - 4√7)/3

  =  (11/3) - (4√7/3)

Hence the value of a is 4/3 and b is 11/3

Question 4 :

If x = √5 + 2, then find the value of x² + 1/x²

Solution :

x = √5 + 2

a² + b²  =  (a + b)² - 2ab 

x² + (1/x)²  =  (x + (1/x))² - 2x(1/x) 

=  (x + (1/x))² - 2  ----(1)

x + (1/x)  = √5 + 2 + (1/(√5 + 2))

 =  ((√5 + 2)² + 1)/(√5 + 2)

 =  (5 + 2 + 4√5 + 1)/(2 + √5)

 =  (8 + 4√5)/(2 + √5)

=  4(2 + √5)/(2 + √5)

=  4

x² + (1/x)²   =  4

By applying the value of x² + (1/x)² in (1), we get

  =  4 - 2 

  =  2

Hence 2 is the answer.

Question 5 :

Given that √2  =  1.414, find the value of (8-5√2)/(3-2√2) (to 3 places of decimals).

Solution :

(8-5√2)/(3-2√2)

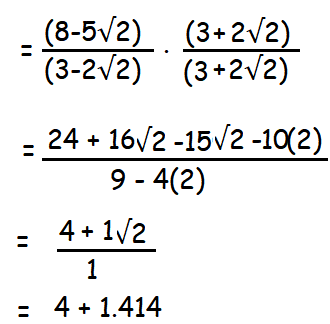
  =  5.414 is the answer

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.